题目内容
1.已知α∈(0,$\frac{π}{2}$),β∈(0,$\frac{π}{2}$),且cosα=$\frac{1}{7}$,cos(α+β)=-$\frac{11}{14}$,则sinβ=$\frac{\sqrt{3}}{2}$.分析 由条件利用同角三角函数的基本关系、两角差的正弦公式,以及三角函数在各个象限中的符号,求得sinβ=sin[(α+β)-α]的值.
解答 解:∵已知α∈(0,$\frac{π}{2}$),β∈(0,$\frac{π}{2}$),且cosα=$\frac{1}{7}$,cos(α+β)=-$\frac{11}{14}$,
∴sinα=$\sqrt{{1-cos}^{2}α}$=$\frac{4\sqrt{3}}{7}$,sin(α+β)=$\sqrt{{1-cos}^{2}(α+β)}$=$\frac{5\sqrt{3}}{14}$,
则sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα
=$\frac{5\sqrt{3}}{14}$•$\frac{1}{7}$-(-$\frac{11}{14}$)•$\frac{4\sqrt{3}}{7}$=$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题主要考查同角三角函数的基本关系、两角差的正弦公式,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
16.已知命题P:?x∈R,ex-x-1>0,则¬P是( )
| A. | ?x∈R,ex-x-1<0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≤0 | ||
| C. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1<0 | D. | ?x∈R,ex-x-1≤0 |
13.已知某三棱锥的三视图(单位:cm)如图所示,那么该三棱锥的体积等于( )
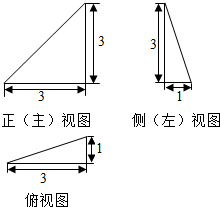

| A. | $\frac{3}{2}$cm3 | B. | 2cm3 | C. | 3cm3 | D. | 9cm3 |
10.已知椭圆$\frac{x^2}{16}+\frac{y^2}{4}$=1过点P(2,1)作弦且弦被P平分,则此弦所在的直线方程为( )
| A. | 2x-y-3=0 | B. | 2x-y-1=0 | C. | x+2y-1=0 | D. | x+2y-4=0 |
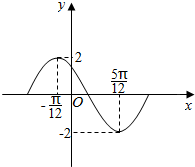 函数y=Asin(ωx+ϕ),(A>0,ω>0,0<ϕ<π)在一个周期内的图象如图所示.
函数y=Asin(ωx+ϕ),(A>0,ω>0,0<ϕ<π)在一个周期内的图象如图所示.