题目内容
数列{an}是等差数列,a1=f(x+1),a2=0,a3=f(x-1),其中f(x)=x2-4x+2,则通项公式an=( )
| A、-2n+4 |
| B、-2n-4 |
| C、2n-4或-2n+4 |
| D、2n-4 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:由已知条件得(x2-2x+1)+(x2-6x+7)=2x2-4x6=0,解得:x=1或x=3 当x=1时a1=-2,此时公差d=2,an=-2+(n-1)×2=2n-4;当x=3时a1=2,公差d=-2,an=2+(n-1)×(-2)=-2n+4.由此能求出结果.
解答:
解:∵f(x)=x2-4x+2,
∴a1=f(x+1)=(x+1)2-4(x+1)+2
=x2-2x-1,
a3=f(x-1)=(x-1)2-4(x-1)+2
=x2-6x+7,
又数列{an}是等差数列,a2=0
∴a1+a3=2a2=0,
∴(x2-2x+1)+(x2-6x+7)=2x2-4x6=0,
解得:x=1或x=3
当x=1时a1=-2,此时公差d=2,an=-2+(n-1)×2=2n-4;
当x=3时a1=2,公差d=-2,an=2+(n-1)×(-2)=-2n+4.
∴an=2n-4或an=-2n+4.
故选:C.
∴a1=f(x+1)=(x+1)2-4(x+1)+2
=x2-2x-1,
a3=f(x-1)=(x-1)2-4(x-1)+2
=x2-6x+7,
又数列{an}是等差数列,a2=0
∴a1+a3=2a2=0,
∴(x2-2x+1)+(x2-6x+7)=2x2-4x6=0,
解得:x=1或x=3
当x=1时a1=-2,此时公差d=2,an=-2+(n-1)×2=2n-4;
当x=3时a1=2,公差d=-2,an=2+(n-1)×(-2)=-2n+4.
∴an=2n-4或an=-2n+4.
故选:C.
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知cos(θ+
)=-
,θ∈(0,
),则cos2θ等于( )
| π |
| 4 |
| ||
| 10 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
抛掷红、黄两颗骰子,当红色骰子的点数为4或6时,两颗骰子的点数之积大于20的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
原点到直线3x+4y+5=0的距离为( )
| A、1 | B、2 | C、3 | D、4 |
设火箭发射成功的概率为0.99,若发射10次,其中失败的次数为X,则E(X)等于( )
| A、0.01 | ||
| B、9.9 | ||
| C、0.1 | ||
D、C
|
若角α的终边在直线y=-2x上,且sina>0,则cosa值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
| D、-2 |
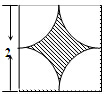 如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )
如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )