题目内容
已知a>0,b>0,
+
=2,求a+b-
的最大值.
| ||
| a |
| 1 |
| b |
| a2+b2 |
考点:基本不等式
专题:三角函数的求值,不等式的解法及应用
分析:如图所示,下面就一般情况给出结论.设P(m,n),∠OAP=θ.θ∈(0,
),可得E=m,EA=
,OA=m+
.OB=n+mtanθ,AB=
+
,于是OA+OB-AB=m+n+mtanθ+
-
-
=2(m+n)-(nx+
),其中x=1+tan
∈(1,2).再利用基本不等式的性质即可得出最大值.把m=
,n=
代入上式可得.
| π |
| 2 |
| n |
| tanθ |
| n |
| tanθ |
| m |
| cosθ |
| n |
| sinθ |
| n |
| tanθ |
| m |
| cosθ |
| n |
| sinθ |
| 2m |
| x |
| θ |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答:
解:∵a>0,b>0,
+
=2,表示直线AB经过点(
,
),A(a,0),B(0,b).
则a+b-
=OA+OB-AB.
如图所示,下面就一般情况给出结论.
设P(m,n),∠OAP=θ.θ∈(0,
),则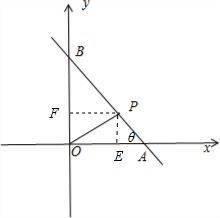
OE=m,EA=
,∴OA=m+
.
同理可得:OB=n+mtanθ,AB=
+
,
∴OA+OB-AB=m+n+mtanθ+
-
-
=m+n-
-
,
=m+n-
-
=m+n-
-ntan
=2(m+n)-(nx+
),其中x=1+tan
∈(1,2).
≤2(m+n)-2
,当且仅当x=
=1+tan
时取等号.
把m=
,n=
代入上式可得:
a+b-
的最大值为2(
+
)-2
=
+1-
.当且仅当
=1+tan
,即1+tan
=
时取等号.
| ||
| a |
| 1 |
| b |
| ||
| 2 |
| 1 |
| 2 |
则a+b-
| a2+b2 |
如图所示,下面就一般情况给出结论.
设P(m,n),∠OAP=θ.θ∈(0,
| π |
| 2 |

OE=m,EA=
| n |
| tanθ |
| n |
| tanθ |
同理可得:OB=n+mtanθ,AB=
| m |
| cosθ |
| n |
| sinθ |
∴OA+OB-AB=m+n+mtanθ+
| n |
| tanθ |
| m |
| cosθ |
| n |
| sinθ |
=m+n-
| m(1-sinθ) |
| cosθ |
| n(1-cosθ) |
| sinθ |
=m+n-
m(cos
| ||||
cos2
|
n2sin2
| ||||
2sin
|
=m+n-
m(1-tan
| ||
1+tan
|
| θ |
| 2 |
=2(m+n)-(nx+
| 2m |
| x |
| θ |
| 2 |
≤2(m+n)-2
| 2mn |
|
| θ |
| 2 |
把m=
| ||
| 2 |
| 1 |
| 2 |
a+b-
| a2+b2 |
| ||
| 2 |
| 1 |
| 2 |
2×
|
| 3 |
2
|
|
| θ |
| 2 |
| θ |
| 2 |
2
|
点评:本题考查了过定点的直线有关最大值问题、三角函数代换问题、三角函数化简、基本不等式的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 为考察中学生的性别与是否喜欢某项运动之间的关系,随机抽取了某校的部分学生进行调查,并将调查数据制作成二维条形图(如图),若已知共有83名学生喜欢此项运动,且男生的喜欢比例比女生多29%,则女生中喜欢此项运动的比例是( )
为考察中学生的性别与是否喜欢某项运动之间的关系,随机抽取了某校的部分学生进行调查,并将调查数据制作成二维条形图(如图),若已知共有83名学生喜欢此项运动,且男生的喜欢比例比女生多29%,则女生中喜欢此项运动的比例是( )| A、35% | B、36% |
| C、64% | D、65% |
已知函数f(x)是定义在R上的奇函数,其导函数为f′(x),当x<0时,2f(x)+xf′(x)<0恒成立,则f(1),2014f(
),2015f(
)在大小关系为( )
| 2014 |
| 2015 |
A、2015f(
| ||||
B、2015f(
| ||||
C、f(1)<2015f(
| ||||
D、f(1)<2014f(
|
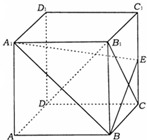 长方体ABCD-A1B1C1D1中,AA1=2,BC=
长方体ABCD-A1B1C1D1中,AA1=2,BC=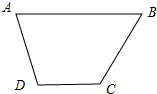 如图,等腰梯形ABCD中,AB∥CD,且AB=2,AD=1,DC=2x(x∈(0,1)),以A,B为焦点,且过点D的双曲线的离心率为e1.以C,D为焦点,且过点A的椭圆的离心率为e1,动点E在边AB上,且|AE|<e1+e2,对x∈(0,1)恒成立,则|AE|的最大值为( )
如图,等腰梯形ABCD中,AB∥CD,且AB=2,AD=1,DC=2x(x∈(0,1)),以A,B为焦点,且过点D的双曲线的离心率为e1.以C,D为焦点,且过点A的椭圆的离心率为e1,动点E在边AB上,且|AE|<e1+e2,对x∈(0,1)恒成立,则|AE|的最大值为( ) 如图,在?ABCD中,E是AD上的一点,且AE=AB,BE和CD的延长线交于点F,且∠BFC=35°,求?ABCD的各内角的度数.
如图,在?ABCD中,E是AD上的一点,且AE=AB,BE和CD的延长线交于点F,且∠BFC=35°,求?ABCD的各内角的度数.