题目内容
7.在菱形ABCD中,∠A=60°,AB=$\sqrt{3}$,将△ABC沿BD折起到△PBD的位置,若平面PBD⊥平面CBD,则三棱锥P-BCD的外接球体积为$\frac{5\sqrt{5}}{6}π$.分析 根据已知,求出三棱锥P-BCD的外接球半径,代入球的体积公式,可得答案.
解答 解:∵菱形ABCD中,∠A=60°,AB=$\sqrt{3}$,
∴BD=$\sqrt{3}$,AC=3,
即△BCD,△BAD是边长为$\sqrt{3}$的等边三角形,其外接圆半径为1,
将△ABC沿BD折起到△PBD的位置,且平面PBD⊥平面CBD,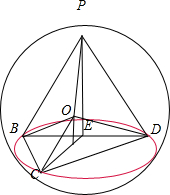
取BD中点E,连接PE,CE,则∠PEC=$\frac{π}{2}$,PE=CE=$\frac{3}{2}$,
则${R}^{2}=(\frac{3}{2}-1)^{2}+(\frac{3}{2}-1)^{2}+(\frac{\sqrt{3}}{2})^{2}$,
解得:R=$\frac{\sqrt{5}}{2}$,
故三棱锥P-BCD的外接球体积V=$\frac{4}{3}{πR}^{3}$=$\frac{5\sqrt{5}}{6}π$,
故答案为:$\frac{5\sqrt{5}}{6}π$
点评 本题考查的知识点是球的内接多面体,球的体积计算,根据已知求出球的半径是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.复数$\frac{3i}{1-i}$(i是虚数单位)的虚部是( )
| A. | $\frac{3}{2}i$ | B. | $\frac{3}{2}$ | C. | $-\frac{3}{2}i$ | D. | $-\frac{3}{2}$ |
17.某企业有甲、乙两个研发小组,为了比较他们的研发水平,若某组成功研发一种新产品,则给该组记1分,否则记0分,现随机抽取这两个小组过去研发新产品15次的成绩如下:
(1)试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;
(2)若该企业安排甲、乙两组各自研发一种新产品,试估算恰有一组研发成功的概率.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 甲 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 乙 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
(2)若该企业安排甲、乙两组各自研发一种新产品,试估算恰有一组研发成功的概率.