题目内容
4．已知函数f（x）=$\frac{x}{4}$+$\frac{a}{x}$-lnx-$\frac{3}{2}$，其中a∈R，若曲线y=f（x）在点（1，f（1））处的切线垂直于直线x-3y=0，则切线方程为3x+y-4=0．分析 由曲线y=f（x）在点（1，f（1））处的切线垂直于直线x-3y=0可得f′（1）=-3，可求出a的值，可得切点坐标，即可求出切线方程．
解答 解：∵f（x）=$\frac{x}{4}$+$\frac{a}{x}$-lnx-$\frac{3}{2}$，
∴f′（x）=$\frac{1}{4}-\frac{a}{{x}^{2}}-\frac{1}{x}$，
∵曲线y=f（x）在点（1，f（1））处的切线垂直于直线x-3y=0，
∴f′（1）=$\frac{1}{4}$-a-1=-3，
解得：a=$\frac{9}{4}$，
∴f（1）=1，
∴切线方程为y-1=-3（x-1），即3x+y-4=0．
故答案为：3x+y-4=0．
点评 本题考查的知识点是利用导数研究曲线上某点切线方程，求出a是关键，难度中档．
练习册系列答案
相关题目
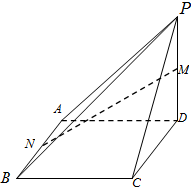如图：在四棱锥P-ABCD中，底面ABCD是矩形，PD⊥平面ABCD，且PD=DA=DC=2．