题目内容
10.在极坐标系中,定点A(2,0),点B在直线$\sqrt{3}$ρcosθ+ρsinθ=0上运动,当线段AB最短时,点B的极坐标为(1,$\frac{5π}{3}$).分析 求出动点B在直线$\sqrt{3}$x+y=0上运动,当线段AB最短时,直线AB垂直于直线$\sqrt{3}$x+y=0,由此能求出点B的极坐标.
解答 解:∵x=ρcosθ,y=ρsinθ,代入直线$\sqrt{3}$ρcosθ+ρsinθ=0,
可得$\sqrt{3}$x+y=0…①,
∵在极坐标系中,定点A(2,0),
∴在直角坐标系中,定点A(2,0),
∵动点B在直线$\sqrt{3}$x+y=0上运动,
∴当线段AB最短时,直线AB垂直于直线$\sqrt{3}$x+y=0,
∴kAB=$\frac{\sqrt{3}}{3}$,
设直线AB为:y=$\frac{\sqrt{3}}{3}$(x-2),即x-$\sqrt{3}y$-2=0,…②,
联立方程①②求得交点B($\frac{1}{2},-\frac{\sqrt{3}}{2}$),
∴ρ=$\sqrt{{x}^{2}+{y}^{2}}$=1,tan$θ=\frac{y}{x}$=$\frac{-\frac{\sqrt{3}}{2}}{\frac{1}{2}}$=-$\sqrt{3}$,∴θ=$\frac{5π}{3}$.
∴点B的极坐标为(1,$\frac{5π}{3}$).
故答案为:(1,$\frac{5π}{3}$).
点评 本题考查点的极坐标的求法,是基础题,解题时要认真审题,注意极坐标和直角坐标互化公式的合理运用.

练习册系列答案
相关题目
15.sin660°=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
20.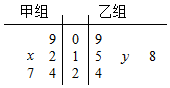 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )
 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )| A. | 18,6 | B. | 8,16 | C. | 8,6 | D. | 18,16 |