题目内容
11.设$\frac{π}{2}$<α<π,若sin(α+$\frac{π}{6}$)=$\frac{1}{3}$,则cos($\frac{2π}{3}$+α)=( )| A. | -$\frac{2\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
分析 利用角的范围可确定三角函数值的符号,利用诱导公式即可求值.
解答 解:∵$\frac{π}{2}$<α<π,$\frac{2π}{3}$<α+$\frac{π}{6}$<$\frac{7π}{6}$,sin(α+$\frac{π}{6}$)=$\frac{1}{3}$>0,
∴$\frac{2π}{3}$<α+$\frac{π}{6}$<π,可得:$\frac{7π}{6}$<$\frac{2π}{3}$+α<$\frac{3π}{2}$,
∴cos($\frac{2π}{3}$+α)=cos[(α+$\frac{π}{6}$)+$\frac{π}{2}$]=-sin(α+$\frac{π}{6}$)=-$\frac{1}{3}$.
故选:C.
点评 本题主要考查了诱导公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列函数中,与函数y=2x表示同一函数的是( )
| A. | y=$\frac{2{x}^{2}}{x}$ | B. | y=$\sqrt{4{x}^{2}}$ | C. | y=($\sqrt{2x}$)2 | D. | y=log24x |
3.设a=21.2,b=log38,c=0.83.1,则( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | a<c<b |
20.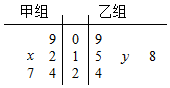 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )
 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )| A. | 18,6 | B. | 8,16 | C. | 8,6 | D. | 18,16 |
1.设全集U={x∈N|x≤8},集合A={1,3,7},B={2,3,8},则(∁UA)∩(∁UB)=( )
| A. | {1,2,7,8} | B. | {4,5,6} | C. | {0,4,5,6} | D. | {0,3,4,5,6} |