题目内容
若圆锥的底面半径为3.侧面展开图的圆心角是60°,则其母线长为 .
考点:旋转体(圆柱、圆锥、圆台)
专题:计算题,空间位置关系与距离
分析:利用圆锥的底面周长等于圆锥的侧面展开图的弧长即可求解.
解答:
解:设母线长为l,则
•l=2π×3
解得:l=18.
故答案为:180.
| π |
| 3 |
解得:l=18.
故答案为:180.
点评:考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
相关题目
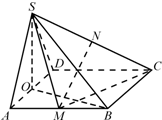 四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N、O分别是AB、SC、AD的中点.
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N、O分别是AB、SC、AD的中点.(Ⅰ)求证:MN∥平面SAD;
(Ⅱ)求证:平面SOB⊥平面SCM.
已知圆C:(x-2)2+y2=1和两点A(0,a)与B(0,-a)(a>0),若圆C上存在一点P使得PA⊥PB,则a的取值范围是( )
| A、(0,3] |
| B、(0,1] |
| C、[1,3] |
| D、[3,+∞) |
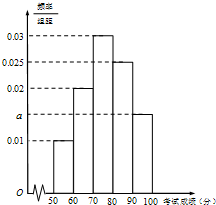 某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.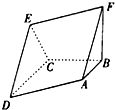 如图空间几何体ABCDEF中,四边形ADEF为平行四边形,FB⊥平面ABCD,AB∥CD,AB⊥BC,AB=BC=
如图空间几何体ABCDEF中,四边形ADEF为平行四边形,FB⊥平面ABCD,AB∥CD,AB⊥BC,AB=BC=