题目内容
某几何体的三视图(单位:cm)如图所示,则该几何体最长棱的棱长为 cm.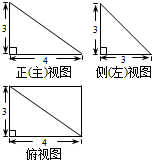

考点:由三视图还原实物图
专题:空间位置关系与距离
分析:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,结合直观图求相关几何量的数据,可得答案.
解答:
 解:由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,如图:
解:由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,如图:
其中PA⊥平面ABCD,∴PA=3,AB=3,AD=4,
∴PB=3
,PC=
=
,PD=5.
该几何体最长棱的棱长为:
.
故答案为:
.
 解:由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,如图:
解:由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,如图:其中PA⊥平面ABCD,∴PA=3,AB=3,AD=4,
∴PB=3
| 2 |
| 32+52 |
| 34 |
该几何体最长棱的棱长为:
| 34 |
故答案为:
| 34 |
点评:本题考查了由三视图求几何体的最长棱长问题,根据三视图判断几何体的结构特征是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中的假命题是( )
| A、?x∈R,lnx=0 |
| B、?x∈R,sinx+cosx=1 |
| C、?x∈R,x3>0 |
| D、?x∈R,3x>0 |
已知圆8:x2+y2-4x-2y-15=0上有两个不同的点到直线l:y=k(x-7)+6的距离等于
,则k的取值范围是( )
| 5 |
A、(
| ||||
B、(-2,-
| ||||
C、(-∞,-2)∪(-
| ||||
D、(-∞,-
|
已知实数x,y满足
,则z=x-y的最小值为( )
|
| A、1 | B、-1 | C、2 | D、-2 |
 已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.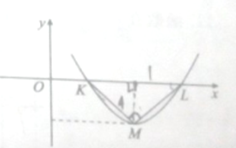 设f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),f(x)为偶函数,且部分图象如图所示,△KML为等腰直角三角形,其中∠KML=90°,|KL|=2.
设f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),f(x)为偶函数,且部分图象如图所示,△KML为等腰直角三角形,其中∠KML=90°,|KL|=2.