题目内容
已知双曲线 -
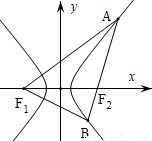
- =1的左右焦点分别为F1,F2,过F2的直线交双曲线右支于A,B两点,且
=1的左右焦点分别为F1,F2,过F2的直线交双曲线右支于A,B两点,且 =3
=3 ,若△ABF1是以B为顶角的等腰三角形,则双曲线的离心率等于( )
,若△ABF1是以B为顶角的等腰三角形,则双曲线的离心率等于( )A.3
B.2
C.

D.

【答案】分析:将向量关系转化为长度关系,然后利用双曲线的定义分别将边长表示为a的关系,然后利用余弦定理建立a,c的方程,从而求出双曲线的离心率.
解答:解:因为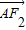 =3
=3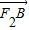 ,所以AF2=3F2B,设BF2=m,则AF2=3m,所以BF2=AB=4m.
,所以AF2=3F2B,设BF2=m,则AF2=3m,所以BF2=AB=4m.
又BF1-BF2=3m=2a,即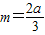 ,
,
所以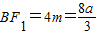 ,
,
又AF1-AF2=AF1-3m=2a,所以AF1=2a+3m=4a.
由余弦定理得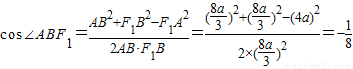 .
.
又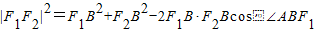 ,
,
即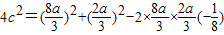 =8a2,
=8a2,
所以c2=2a2,即c=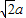 ,即离心率e=
,即离心率e=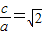 .
.
故选D.
点评:本题主要考查双曲线的定义以及余弦定理的应用,将向量关系转化为长度关系,利用余弦定理求出边长和a,c之间的关系是解决本题的关键.本题运算量较大,综合性较强,考查学生的运算能力.
解答:解:因为
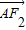 =3
=3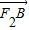 ,所以AF2=3F2B,设BF2=m,则AF2=3m,所以BF2=AB=4m.
,所以AF2=3F2B,设BF2=m,则AF2=3m,所以BF2=AB=4m.又BF1-BF2=3m=2a,即
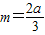 ,
,所以
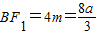 ,
,又AF1-AF2=AF1-3m=2a,所以AF1=2a+3m=4a.
由余弦定理得
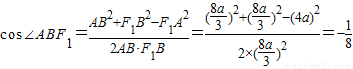 .
.又
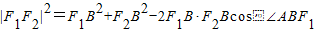 ,
,即
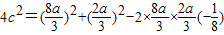 =8a2,
=8a2,所以c2=2a2,即c=
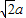 ,即离心率e=
,即离心率e=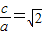 .
.故选D.

点评:本题主要考查双曲线的定义以及余弦定理的应用,将向量关系转化为长度关系,利用余弦定理求出边长和a,c之间的关系是解决本题的关键.本题运算量较大,综合性较强,考查学生的运算能力.

练习册系列答案
相关题目