题目内容
已知双曲线
-
=1的左、右焦点为F1、F2，左准线为l，试问：能否在双曲线的左支上找到一点P，使得|PF1|是P到l的距离d与|PF2|的等比中项？并说明理由.
思路解析：解题方法相当于反证法，假设满足条件的点P存在，则由条件出发，或求出点P，或导出予盾，最后得出结论.双曲线左分支上的点P到左焦点F1的距离的最小值是c-a，到右焦点F2距离的最小值是c+a. 解法一：如上图所示，假设双曲线左支上存在一点P（x0,y0），使得 由第二定义， 由焦半径公式,得e( 即a-ex0=e(-a-ex0)，解得x0= ∵a=5,b=12,∴c=13,e= ∵点P在双曲线的左支上，∴x0≤-a=-5.但- ∴满足条件的点P不存在. 解法二：由解法一得|PF2|=e|PF1|， ① 又由双曲线的定义，有|PF2|-|PF1|=2a. ② 消去|PF2|得|PF1|= ∵P在双曲线的左支上， ∴|PF1|≥c-a=13-5=8. 但是 解法三：由解法二中的①、②两式联立,解得|PF1|= ∴|PF1|+|PF2|= 但|PF1|+|PF2|≥|F1F2|=26, ∵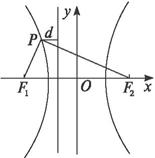
=
成立.
=e,∴|PF2|=e|PF1|.
-x0)=e·e(-
-x0),
.
.代入计算得x0=-
.
＞-5.
=
.
＜8,∴满足条件的点P不存在.
=
,|PF2|=
=
.
.
＜26,∴满足条件的点P不存在.
初中自主学习课时集训系列答案
过关冲刺100分系列答案
圆梦图书课时达标100分系列答案
高效作业系列答案
倍速学习法系列答案
-
=1的左焦点为F1,左,右顶点为A1,A2,P为双曲线上任意一点,则分别以线段PF1,A
=1的左焦点为F1，左、右顶点为A1、A2，P为双曲线上任意一点，则分别以线段PF1、A1A2为直径的两个圆的位置关系为（ ）
=1的左支上有一点M，右焦点为F,N是MF的中点，且|ON|=4，则M到右准线的距离为 ( )
C．
D．
=1的左、右焦点分别为F1、F2，点P为双曲线上一点，|OP|=
，|PF1|、|F1F2|、|PF2|成等比数列，求最小的自然数b的值.