题目内容
20.已知等差数列{an}的前n项和Sn满足S3=0,S5=-5.则数列$\left\{{\frac{1}{{{a_{2n-1}}{a_{2n+1}}}}}\right\}$的前50项和T50=$\frac{-51}{101}$.分析 设等差数列{an}的公差为d,由S3=0,S5=-5.可得$3{a}_{1}+\frac{3×2}{2}$d=0,$5{a}_{1}+\frac{5×4}{2}$d=-5,解得a1,d.可得an=2-n.可得$\frac{1}{{a}_{2n-1}{a}_{2n+1}}$=$\frac{1}{2}(\frac{1}{2n-3}-\frac{1}{2n-1})$,利用“裂项求和方法”即可得出.
解答 解:设等差数列{an}的公差为d,∵S3=0,S5=-5.
∴$3{a}_{1}+\frac{3×2}{2}$d=0,$5{a}_{1}+\frac{5×4}{2}$d=-5,
解得a1=1,d=-1.
∴an=1-(n-1)=2-n.
∴$\frac{1}{{a}_{2n-1}{a}_{2n+1}}$=$\frac{1}{(2n-3)(2n-1)}$=$\frac{1}{2}(\frac{1}{2n-3}-\frac{1}{2n-1})$,
则数列$\left\{{\frac{1}{{{a_{2n-1}}{a_{2n+1}}}}}\right\}$的前50项和T50=$\frac{1}{2}[(-1-1)+(1-\frac{1}{3})$+…+$(\frac{1}{99}-\frac{1}{101})]$
=$\frac{1}{2}(-1-\frac{1}{101})$
=$\frac{-51}{101}$.
故答案为:$\frac{-51}{101}$.
点评 本题考查了裂项求和方法、等差数列的通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
10.已知抛物线${x^2}=-4\sqrt{5}y$的焦点与双曲线$\frac{x^2}{a}+\frac{y^2}{4}=1(a∈R)$的一个焦点重合,则该双曲线的渐近线方程为( )
| A. | y=±2x | B. | y=±4x | C. | $y=±\frac{1}{4}x$ | D. | $y=±\frac{1}{2}x$ |
11.已知全集U=R,集合A={x|x2>4},则∁UA=( )
| A. | (-∞,-2)∪(2,+∞) | B. | [-2,2] | C. | (-∞,-4)∪(4,+∞) | D. | [-4,4] |
8.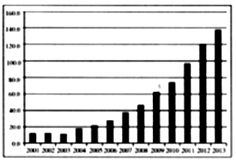 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=aax+b | D. | y=alnx+b |
5.函数f(x)的定义域为R,导函数f'(x)的图象如图所示,则函数f(x)( )
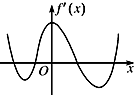

| A. | 无极大值点,有四个极小值点 | B. | 有三个极大值点,两个极小值点 | ||
| C. | 有两个极大值点,两个极小值点 | D. | 有四个极大值点,无极小值点 |
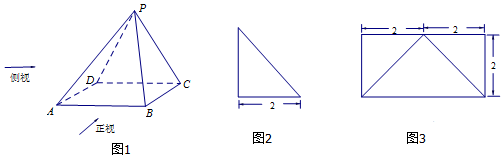
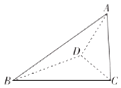 已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=$\sqrt{3}$,BC=2,CD=$\sqrt{5}$,则球O的表面积为12π.
已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=$\sqrt{3}$,BC=2,CD=$\sqrt{5}$,则球O的表面积为12π.


