题目内容
1.在△ABC中,角A,B,C所对的边分别为a,b,c.函数f(x)=sin(2x+A).(1)若$A=\frac{π}{2}$,则$f(-\frac{π}{6})$的值为$\frac{1}{2}$;
(2)若$f(\frac{π}{12})=1$,a=3,$cosB=\frac{4}{5}$,求△ABC的边b的长度.
分析 (1)由已知利用诱导公式,特殊角的三角函数值即可得计算得解.
(2)由$f(\frac{π}{12})=1$,可得$2×\frac{π}{12}+A=2kπ+\frac{π}{2}(k∈Z)$,结合范围0<A<π,可求A,
由$cosB=\frac{4}{5}$,结合范围0<B<π,利用同角三角函数基本关系式可求sinB的值,进而利用正弦定理可求b的值.
解答 解:(1)若$A=\frac{π}{2}$,则$f(-\frac{π}{6})$=sin[2×(-$\frac{π}{6}$)+$\frac{π}{2}$]=sin$\frac{π}{6}$=$\frac{1}{2}$.…(2分)
故答案为:$\frac{1}{2}$.
(2)f(x)=sin(2x+A)且$f(\frac{π}{12})=1$,
则$2×\frac{π}{12}+A=2kπ+\frac{π}{2}(k∈Z)$,
注意到0<A<π,所以$k=0,A=\frac{π}{3}$.…(3分)
因为$cosB=\frac{4}{5}$,0<B<π,所以$sinB=\frac{3}{5}$.
在△ABC中,由正弦定理得$\frac{b}{sinB}=\frac{a}{sinA}⇒\frac{b}{{\frac{3}{5}}}=\frac{3}{{sin\frac{π}{3}}}⇒b=\frac{{6\sqrt{3}}}{5}$.…(5分)
点评 本题主要考查了诱导公式,特殊角的三角函数值,同角三角函数基本关系式,正弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
9.已知a=0.78,b=80.7,c=log0.78,则a、b、c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
16.与直线 $y=\frac{1}{2}x+1$垂直,且过(2,0)点的直线方程是( )
| A. | y=-2x+4 | B. | $y=\frac{1}{2}x-1$ | C. | y=-2x-4 | D. | $y=\frac{1}{2}x-4$ |
6.函数f(x)=$\frac{{e}^{2x}}{x}$的导函数为( )
| A. | f′(x)=2e2x | B. | f′(x)=$\frac{(2x-1){e}^{2x}}{{x}^{2}}$ | C. | f′(x)=$\frac{2{e}^{2x}}{x}$ | D. | f′(x)=$\frac{(x-1){e}^{2x}}{{x}^{2}}$ |
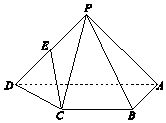 如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1
如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1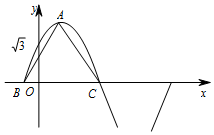 已知函数$f(x)=Asin({ωx+φ})({A>0\;,\;\;ω>0\;,\;\;|φ|<\frac{π}{2}})$在一个周期内的图象如图所示,图象过点$({0\;,\;\;\sqrt{3}})$,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为高为$2\sqrt{3}$的正三角形.
已知函数$f(x)=Asin({ωx+φ})({A>0\;,\;\;ω>0\;,\;\;|φ|<\frac{π}{2}})$在一个周期内的图象如图所示,图象过点$({0\;,\;\;\sqrt{3}})$,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为高为$2\sqrt{3}$的正三角形.