题目内容
在三角形△ABC中,若
+
<sinC,则三角形ABC的形状是 三角形.
| asinA |
| c |
| bsinB |
| c |
考点:三角形的形状判断
专题:计算题
分析:通过已知表达式,利用正弦定理与勾股定理即可判断三角形的形状.
解答:
解:因为在三角形△ABC中,若
+
<sinC,
所以由正弦定理并化简得:a2+b2<c2,
由余弦定理a2+b2-c2=2abcosC,所以cosC<0,所以三角形是钝角三角形.
故答案为:钝角.
| asinA |
| c |
| bsinB |
| c |
所以由正弦定理并化简得:a2+b2<c2,
由余弦定理a2+b2-c2=2abcosC,所以cosC<0,所以三角形是钝角三角形.
故答案为:钝角.
点评:本题考查三角形的形状的判断,正弦定理与勾股定理的应用,考查计算能力.

练习册系列答案
相关题目
已知A,B,C为圆O上三点,线段CO的延长线与线段AB有交点,若
=m
+n
,则m+n的范围是( )
| OC |
| OA |
| OB |
| A、(0,1) |
| B、(1,+∞) |
| C、(-1,0) |
| D、(-∞,-1) |
二次函数y=a(a+1)x2-(2a+1)x+1,当a=1,2,3,…,n,…时,其图象在x轴上截得的弦长依次为d1,d2,…,dn,…,则d1+d2+…+dn为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
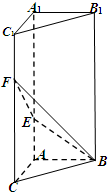 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中, 如图,AB为半圆的直径,P为半圆上一点,|AB|=10,∠PAB=a,且sina=
如图,AB为半圆的直径,P为半圆上一点,|AB|=10,∠PAB=a,且sina=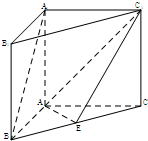 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.