题目内容

下列不等式成立的是（　　）
A、sin130°＜sin140°
B、sin130°＞sin140°
C、cos130°＜cos140°
D、tan130°＞tan140°
考点：三角函数线
专题：三角函数的图像与性质
分析：由条件根据三角函数在（90°，180°）上的单调性，可得结论．
解答： 解：由于y=sinx在（90°，180°）上是减函数，130°＜140°，∴sin130°＞sin140°，
故A不正确、B正确．
由于y=cosx在（90°，180°）上是减函数，130°＜140°，∴cos130°＞cos140°，故C不正确．
y=tanx在（90°，180°）上是增函数，130°＜140°，∴tan130°＜tann140°，故D不正确，
故选：B．
点评：本题主要考查三角函数在（90°，180°）上的单调性，属于基础题．
练习册系列答案
相关题目
（文科实验做）F1、F2是双曲线的左右焦点，P是双曲线上一点，且∠F1PF2=60°，S△PF1F2=12
3
，离心率为2．求双曲线的方程．
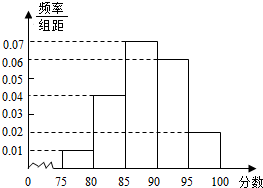某工厂招聘工人，在一次大型的招聘中，其中1000人的笔试成绩的频率分布直方图如图所示，按厂方规定85分以上（含85分）可以直接录用．
（1）下表是这次笔试成绩的频数分布表，求正整数a，b的值；
区间[75，80）[80，85）[85，90）[90，95）[95，100）
人数50a350300b
（2）现在用分层抽样的方法从这1000人中抽取40人的笔试成绩进行分析，求可以直接录用的人数；
（3）在（2）中抽取的40名招聘的人中，随机选取2名参加面试，记“可以直接录用的人数”为X，求X的分布列与数学期望．
已知函数f（x）=mx2+nx-2（m＞0，n＞0）的一个零点是2，则
1
m
+
2
n
的最小值为
 
．
若log2（log5x）=0，则x=
 
．
已知Sn=
1
1×2
+
1
2×3
+
1
3×4
+…+
1
n(n+1)
，若Sn=
9
10
，则n=
 
．
在直角三角形ABC中，∠C=
π
2
，AC=3，取点D使
BD
=2
DA
，那么
CD
•
CA
=（　　）
A、3B、4C、5D、6
已知三棱锥S-ABC中，SA⊥面ABC，AB⊥BC，SA=AB=1，BC=
2
，则此三棱锥外接球的体积为
 
．
若?x∈（0，
1
2
），均有9x＜logax（a＞0，且a≠1），则实数a的取值范围是（　　）
A、[2 -
1
3
，1）
B、（0，2 -
1
3
]
C、（2 
1
3
，3）
D、（1，2 
1
3
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网