题目内容
1.已知函数f(x)=x2-1g(10x+10),若0<b<1,则f(b)的值满足( )| A. | f(b)>f(-$\frac{9}{10}$) | B. | f(b)>0 | C. | f(b)>f($\frac{3}{2}$) | D. | f(b)<f($\frac{3}{2}$) |
分析 根据函数与方程之间的关系,转化为两个函数的大小比较,结合数形结合进行比较即可得到结论.
解答 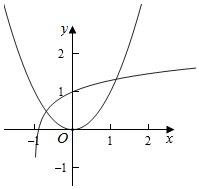 解:f(x)=x2-1g(10x+10)=x2-1g(x+1)-1,
解:f(x)=x2-1g(10x+10)=x2-1g(x+1)-1,
则由x+1>0得x>-1,即函数的定义域为(-1,+∞),
设g(x)=x2,h(x)=1g(10x+10)=1+lg(x+1),
当0<x<1时,0<g(x)<1,
h(x)在0<x<1上为增函数,则1<h(x)<1+lg2,
则此时h(x)>g(x),
即f(x)=g(x)-h(x)<0,即f(b)<0,则B错误.
当0<x<1时,g(x)<h(x),即此时f(x)<0,
即当0<b<1,则f(b)<0,
当x=$\frac{3}{2}$时,f($\frac{3}{2}$)=($\frac{3}{2}$)2-1g(10•$\frac{3}{2}$+10)=$\frac{9}{4}$-lg25>0,
则f(b)<f($\frac{3}{2}$),
故选:D.
点评 本题主要考查函数值的大小比较,利用函数与方程的关系转化为两个函数的大小比较,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
6.若圆锥的侧面展开图的圆心角为90°,半径为r,则该圆锥的全面积为( )
| A. | $\frac{π{r}^{2}}{16}$ | B. | $\frac{3π{r}^{2}}{16}$ | C. | $\frac{π{r}^{2}}{4}$ | D. | $\frac{5π{r}^{2}}{16}$ |
13.在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AC}$=$\overrightarrow{n}$,若点D满足$\overrightarrow{BD}$=2$\overrightarrow{DC}$,则$\overrightarrow{AD}$=( )
| A. | $\frac{1}{3}\overrightarrow{n}$+$\frac{2}{3}\overrightarrow{m}$ | B. | $\frac{5}{3}$$\overrightarrow{m}$-$\frac{2}{3}\overrightarrow{n}$ | C. | $\frac{2}{3}\overrightarrow{n}$-$\frac{1}{3}\overrightarrow{m}$ | D. | $\frac{2}{3}\overrightarrow{n}$+$\frac{1}{3}\overrightarrow{m}$ |
10.曲线f(x)=$\frac{-4}{\sqrt{3}({e}^{x}+1)}$在点(0,f(0))处的切线方程为( )
| A. | x-$\sqrt{3}$y-2=0 | B. | $\sqrt{3}$x+y-2=0 | C. | x-$\sqrt{3}$y+2=0 | D. | $\sqrt{3}$x+y+2=0 |