题目内容
13.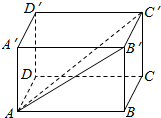 如图,长方体ABCD-A′B′C′D′中,化简下列各式,并在图中标出化简得到的向量:
如图,长方体ABCD-A′B′C′D′中,化简下列各式,并在图中标出化简得到的向量:(1)$\overrightarrow{AA′}$-$\overrightarrow{CB}$;
(2)$\overrightarrow{AB′}$+$\overrightarrow{B′C′}$+$\overrightarrow{C′D′}$;
(3)$\frac{1}{2}$$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{A′A}$.
分析 (1)$\overrightarrow{AA′}$-$\overrightarrow{CB}$=$\overrightarrow{CC′}$-$\overrightarrow{CB}$=$\overrightarrow{BC′}$;
(2)$\overrightarrow{AB′}$+$\overrightarrow{B′C′}$+$\overrightarrow{C′D′}$=$\overrightarrow{AD′}$;
(3)$\frac{1}{2}$$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{A′A}$=$\frac{1}{2}$($\overrightarrow{AD}$+$\overrightarrow{AB}$-$\overrightarrow{A′A}$).
解答 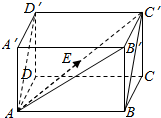 解:(1)$\overrightarrow{AA′}$-$\overrightarrow{CB}$=$\overrightarrow{CC′}$-$\overrightarrow{CB}$=$\overrightarrow{BC′}$;
解:(1)$\overrightarrow{AA′}$-$\overrightarrow{CB}$=$\overrightarrow{CC′}$-$\overrightarrow{CB}$=$\overrightarrow{BC′}$;
(2)$\overrightarrow{AB′}$+$\overrightarrow{B′C′}$+$\overrightarrow{C′D′}$=$\overrightarrow{AD′}$;
(3)$\frac{1}{2}$$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{A′A}$
=$\frac{1}{2}$($\overrightarrow{AD}$+$\overrightarrow{AB}$-$\overrightarrow{A′A}$)
=$\frac{1}{2}$($\overrightarrow{AC}$-$\overrightarrow{A′A}$)
=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{AA′}$)
=$\frac{1}{2}$$\overrightarrow{AC′}$=$\overrightarrow{AE}$.
点评 本题考查了空间向量的线性运算的应用及数形结合的思想应用.

 如图,设正方体ABCD-A1B1C1D1中,M为AA1上点,A1M:MA=3:1,求截面B1D1M与底面ABCD所成二面角.
如图,设正方体ABCD-A1B1C1D1中,M为AA1上点,A1M:MA=3:1,求截面B1D1M与底面ABCD所成二面角.