题目内容
1.设函数f(x)=$\overrightarrow{m}$$•\overrightarrow{n}$,其中向量$\overrightarrow{m}$=(2cosx,1),$\overrightarrow{n}$=(cosx,$\sqrt{3}$sin2x),x∈R.(1)求f(x)的单调递增区间;
(2)求f(x)在[0,$\frac{π}{2}$]上的最大值和最小值.
分析 根据向量数量积的坐标表示式,再用降幂公式和辅助角公式化简整理,可得f(x)=2sin(2x+$\frac{π}{6}$)+1,最后根据函数y=Asin(ωx+φ)+k的单调增区间和最值即可得到本题的答案.
解答 解:(1)f(x)=$\overrightarrow{m}$$•\overrightarrow{n}$,其中向量$\overrightarrow{m}$=(2cosx,1),$\overrightarrow{n}$=(cosx,$\sqrt{3}$sin2x),
∴f(x)=2cos2x+$\sqrt{3}$sin2x=cos2x+$\sqrt{3}$sin2x-1=2sin(2x+$\frac{π}{6}$)+1,
∴-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z,
∴-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,k∈Z,
∴f(x)的单调递增区间为[-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ],k∈Z,
(2)由(1)可知,f(x)在[0,$\frac{π}{6}$]为增函数,在[$\frac{π}{6}$,$\frac{π}{2}$]上为减函数,
∴当x=$\frac{π}{6}$,函数有最大值,即为2+1=3,
f(0)=2sin$\frac{π}{6}$+1=2,f($\frac{π}{2}$)=2sin(π+$\frac{π}{6}$)+1=-1+1=0,
∴f(x)的最小值为0.
点评 本题以向量的数量积运算为载体,着重考查了三角恒等变换、三角函数的图象与性质等知识,属于基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
11.函数f(x)=1-cos2x的周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
9.cosα+$\sqrt{3}$sinα的值是( )
| A. | $\frac{1}{2}$sin($\frac{π}{6}$+α) | B. | 2sin($\frac{π}{3}$+α) | C. | 2sin($\frac{π}{6}$+α) | D. | $\frac{1}{2}$cos($\frac{π}{3}$+α) |
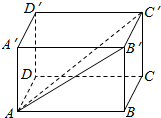 如图,长方体ABCD-A′B′C′D′中,化简下列各式,并在图中标出化简得到的向量:
如图,长方体ABCD-A′B′C′D′中,化简下列各式,并在图中标出化简得到的向量: