题目内容
若不等式|2x+m|≥4-|2x-2|对任意x∈R恒成立,则实数m的取值范围为 .
考点:函数恒成立问题
专题:不等式的解法及应用
分析:将不等式进行等价转化,利用绝对值的意义求出|x+
|+|x-1|的最小值,即可求得实数m的取值范围.
| m |
| 2 |
解答:
解:不等式|2x+m|≥4-|2x-2|等价为|2x+m|+|2x-2|≥4,
即|x+
|+|x-1|≥2恒成立,
|x+
|+|x-1|在数轴上表示到1和-
的距离之和,显然最小距离和就是1到-
的距离,
最小值为d=|1-(-
)|=|1+
|,
∵不等式|x+
|+|x-1|≥2恒成立对任意实数x恒成立,
∴|1+
|≥2
∴1+
≥2或1+
≤-2,
∴m≥2或m≤-6.
∴实数m的取值范围为(-∞,-6]∪[2,+∞),
故答案为:(-∞,-6]∪[2,+∞).
即|x+
| m |
| 2 |
|x+
| m |
| 2 |
| m |
| 2 |
| m |
| 2 |
最小值为d=|1-(-
| m |
| 2 |
| m |
| 2 |
∵不等式|x+
| m |
| 2 |
∴|1+
| m |
| 2 |
∴1+
| m |
| 2 |
| m |
| 2 |
∴m≥2或m≤-6.
∴实数m的取值范围为(-∞,-6]∪[2,+∞),
故答案为:(-∞,-6]∪[2,+∞).
点评:本题主要考查不等式恒成立问题,考查绝对值的意义,解题的关键是利用绝对值的意义求出|x+
|+|x-1|的最小值,是解决本题的关键.
| m |
| 2 |

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
圆(x+2)2+y2=5关于坐标原点(0,0)对称的圆的方程是( )
| A、x2+(y-2)2=5 |
| B、x2+(y+2)2=5 |
| C、(x-2)2+y2=5 |
| D、(x-2)2+(y-2)2=5 |
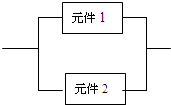 某个部件由两个电子元件按如图连接而成,当元件1或元件2正常工作,该部件正常工作.设两个电子元件的使用寿命(单位:小时)均服从正态分布N(800,100),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过800小时的概率为
某个部件由两个电子元件按如图连接而成,当元件1或元件2正常工作,该部件正常工作.设两个电子元件的使用寿命(单位:小时)均服从正态分布N(800,100),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过800小时的概率为