题目内容

圆（x+2）2+y2=5关于坐标原点（0，0）对称的圆的方程是（　　）
A、x2+（y-2）2=5
B、x2+（y+2）2=5
C、（x-2）2+y2=5
D、（x-2）2+（y-2）2=5
考点：圆的标准方程
专题：
分析：求出已知圆的圆心和半径，求出圆心A关于原点对称的圆的圆心B的坐标，即可得到对称的圆的标准方程．
解答： 解：圆（x+2）2+y2=5的圆心A（-2，0），半径等于
5
，
∴圆心A关于原点（0，0）对称的圆的圆心B（2，0），
所求对称圆的方程为 （x-2）2+y2=5，
故选：C
点评：本题考查求一个圆关于一个点的对称圆的方程的求法，求出圆心A关于原点（0，0）对称的圆的圆心B的坐标，是解题的关键．本题是一个基础题．
练习册系列答案
相关题目
若不等式|2x+m|≥4-|2x-2|对任意x∈R恒成立，则实数m的取值范围为
 
．
集合{a，b}的子集个数
 
．
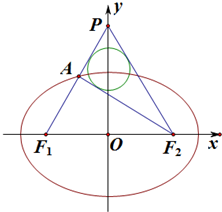已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点分别为F1，F2，|F1F2|=
10
，P是y轴正半轴上一点，PF1交椭圆于点A，若AF2⊥PF1，且△APF2的内切圆半径为
2
2
，则椭圆的离心率是（　　）
A、
5
4
B、
5
3
C、
5
10
D、
15
4
已知向量
a
=（2，3），
b
=（1，4），
c
=（k，3），（
a
+
b
）⊥
c
，则实数k=（　　）
A、-7B、-2C、2D、7
求函数f（x）=x2+
1
x
（x＞0）的单调区间．
已知函数f（x）=x2+ax，若f（x）是定义在（-1，1）上的减函数，且f（a-1）＞f（2a），求a的取值范围．
设数列{an}满足a1=2，a2+a4=8，且对任意的n∈N*，都有an+an+2=2an+1
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列{bn}的前n项和为Sn．且满足S1•Sn=2bn-b1，n∈N*，b1≠0，求数列{anbn}的前n项和Tn．
已知函数f（x）=ax2-4x-1．
（1）当a=2时，求函数f（x）的零点；
（2）当a=2且x∈（0，1）时，f（1-m）-f（2m-1）＜0恒成立，求m的取值范围；
（3）若a=0，设g(x)=
b
x
(b≠0)，且函数h（x）=g（x）-f（x）是区间（1，3）上的单调函数，求b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网