题目内容
已知椭圆C:
+
=1(a>b>0)上有两点A、B,直线l:y=x+k上有两点C、D,四边形ABCD是正方形,此正方形外接圆的方程为x2+y2-2y-8=0,求椭圆C及直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:直线AB的方程设为y=x+m,圆心O(0,1)到直线AB的距离
=
,解得m=4或m=-2.由此利用分类讨论思想能求出椭圆C及直线l的方程.
| |1-0+m| | ||
|
3
| ||
| 2 |
解答:
解:∵ABCD为正方形,CD在直线l:y=x+k上,
∴直线AB的方程设为y=x+m,
圆x2+y2-2y-8=0化为标准方程为x2+(y-1)2=9,
圆心O(0,1),半径r=3,
∵ABCE是圆O的内接正方形
∴圆心O(0,1)到直线AB的距离为
,
由点到直线的距离公式得
=
,
解得m=4或m=-2.
①当m=4时,直线AB与圆O联立
,
解得交点A(-3,1),B(4,0)
代入椭圆椭圆C:
+
=1,解得a=
,b=4,
∵a<b,∴不合题意,舍去.
②当m=-2时,直线AB与圆O联立
,
解得交点A(0,-2),B(3,1)
代入椭圆椭圆C:
+
=1,解得a=2
,b=2
∴椭圆C:
+
=1,
∵直线l和直线AB平行且到O的距离均为
,且不重合,
∴m=-2,k=4
∴直线l:y=x+4.
∴直线AB的方程设为y=x+m,
圆x2+y2-2y-8=0化为标准方程为x2+(y-1)2=9,
圆心O(0,1),半径r=3,
∵ABCE是圆O的内接正方形
∴圆心O(0,1)到直线AB的距离为
3
| ||
| 2 |
由点到直线的距离公式得
| |1-0+m| | ||
|
3
| ||
| 2 |
解得m=4或m=-2.
①当m=4时,直线AB与圆O联立
|
解得交点A(-3,1),B(4,0)
代入椭圆椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
| 12 | ||
|
∵a<b,∴不合题意,舍去.
②当m=-2时,直线AB与圆O联立
|
解得交点A(0,-2),B(3,1)
代入椭圆椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
∴椭圆C:
| x2 |
| 12 |
| y2 |
| 4 |
∵直线l和直线AB平行且到O的距离均为
3
| ||
| 2 |
∴m=-2,k=4
∴直线l:y=x+4.
点评:本题考查椭圆方程及直线方程的求法,解题时要认真审题,注意点到直线的距离公式和分类讨论思想的合理运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
甲船在早6点至12点之间的任意时刻出发,则它早于8点出发的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
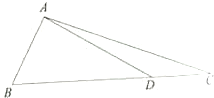 如图,△ABC中,D在边BC上,BD=2,CD=1,AD=
如图,△ABC中,D在边BC上,BD=2,CD=1,AD=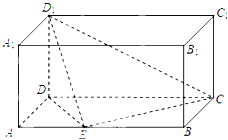 在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点,且不为中点.
在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点,且不为中点.