题目内容
为了应对新疆暴力恐怖活动,重庆市警方从武警训练基地挑选反恐警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选.假定某基地有4名武警战士(分别记为A、B、C、D)拟参加挑选,且每人能通过体能、射击、爆破的概率分别为
,
,
.这三项测试能否通过相互之间没有影响.
(1)求A能够入选的概率;
(2)规定:按入选人数得训练经费,每入选1人,则相应的训练基地得到5000元的训练经费,求该基地得到训练经费的分布列与数学期望(期望精确到个位).
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
(1)求A能够入选的概率;
(2)规定:按入选人数得训练经费,每入选1人,则相应的训练基地得到5000元的训练经费,求该基地得到训练经费的分布列与数学期望(期望精确到个位).
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(I)设A通过体能、射击、爆破分别记为事件M,N,P,且P(M)=
,P(N)=
,P(P)=
,由此能求出A能够入选的概率.
(Ⅱ)记X表示该训练基地入选人数,则得到的训练经费为Y=5000X,又X可能的取值为0,1,2,3,4.分别求出相应在的概率,由此能求出该基地得到训练经费的分布列与数学期望.
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
(Ⅱ)记X表示该训练基地入选人数,则得到的训练经费为Y=5000X,又X可能的取值为0,1,2,3,4.分别求出相应在的概率,由此能求出该基地得到训练经费的分布列与数学期望.
解答:
解:(I)设A通过体能、射击、爆破分别记为事件M,N,P,
且P(M)=
,P(N)=
,P(P)=
,
∴A能够入选的概率:
p=P(MN
)+P(M
P)+P(
NP)+P(MNP)
=
×
×
+
×
×
+
×
×
+
×
×
=
.
(Ⅱ)记X表示该训练基地入选人数,则得到的训练经费为Y=5000X,
又X可能的取值为0,1,2,3,4.
P(X=0)=
(
)0(
)4=
,
P(X=1)=
(
)(
)3=
,
P(X=2)=
(
)2(
)2=
,
P(X=3)=
(
)3(
)=
,
P(X=4)=
(
)4•(
)0=
,
∴训练经费Y=5000X的分布列为:
EY=0×
+5000×
+10000×
+15000×
+20000×
≈13333(元).
且P(M)=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
∴A能够入选的概率:
p=P(MN
. |
| P |
. |
| N |
. |
| M |
=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
=
| 2 |
| 3 |
(Ⅱ)记X表示该训练基地入选人数,则得到的训练经费为Y=5000X,
又X可能的取值为0,1,2,3,4.
P(X=0)=
| C | 0 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 81 |
P(X=1)=
| C | 1 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 81 |
P(X=2)=
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 24 |
| 81 |
P(X=3)=
| C | 3 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 32 |
| 81 |
P(X=4)=
| C | 4 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 16 |
| 81 |
| X | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| Y=5000X | 0 | 5000 | 10000 | 15000 | 20000 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 81 |
| 8 |
| 81 |
| 24 |
| 81 |
| 32 |
| 81 |
| 16 |
| 81 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和期望的求法,是中档题,在历年高考中都有是必考题型.

练习册系列答案
相关题目
log
sin
π+log
cos
π的值是( )
| 2 |
| 5 |
| 12 |
| 2 |
| 5 |
| 12 |
| A、4 | B、1 | C、-4 | D、-1 |
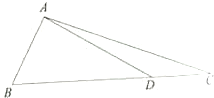 如图,△ABC中,D在边BC上,BD=2,CD=1,AD=
如图,△ABC中,D在边BC上,BD=2,CD=1,AD=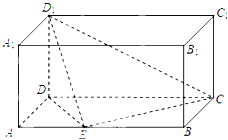 在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点,且不为中点.
在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点,且不为中点.