题目内容
在下列命题中:
①函数f(x)=x+
(x>0)的最小值为2
;
②已知定义在R上周期为4的函数f(x)满足f(2-x)=f(2+x),则f(x)一定为偶函数;
③定义在R上的函数f(x)既是奇函数又是以2为周期的周期函数,则f(1)+f(4)+f(7)=0;
④已知函数f(x)=ax3+bx2+cx+d(d≠0),则a+b+c=0是f(x)有极值的必要不充分条件;
⑤已知函数f(x)=x-sinx,若a+b>0,则f(a)+f(b)>0.
其中正确命题的序号为 (写出所有正确命题的序号).
①函数f(x)=x+
| a |
| x |
| a |
②已知定义在R上周期为4的函数f(x)满足f(2-x)=f(2+x),则f(x)一定为偶函数;
③定义在R上的函数f(x)既是奇函数又是以2为周期的周期函数,则f(1)+f(4)+f(7)=0;
④已知函数f(x)=ax3+bx2+cx+d(d≠0),则a+b+c=0是f(x)有极值的必要不充分条件;
⑤已知函数f(x)=x-sinx,若a+b>0,则f(a)+f(b)>0.
其中正确命题的序号为
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①,由函数f(x)=x+
(x>0),知a≤0时,在f(x)在(0,+∞)为单调递增函数,不存在最小值,可判断①;
②,利用函数的对称性与周期性可得到f(-x)=f(x),从而可判断②;
③,依题意可求得f(4)=0;f(7)=f(-1)=-f(1),从而可判断③;
④,利用导数法及充分必要条件的概念可判断④;
⑤,易求f′(x)=1-cosx≥0,可得f(x)=x-sinx为R上的增函数,进一步可知,f(x)为R上的为奇函数,从而可判断⑤.
| a |
| x |
②,利用函数的对称性与周期性可得到f(-x)=f(x),从而可判断②;
③,依题意可求得f(4)=0;f(7)=f(-1)=-f(1),从而可判断③;
④,利用导数法及充分必要条件的概念可判断④;
⑤,易求f′(x)=1-cosx≥0,可得f(x)=x-sinx为R上的增函数,进一步可知,f(x)为R上的为奇函数,从而可判断⑤.
解答:
解:①,函数f(x)=x+
(x>0)中,
当a≤0时,在f(x)在(0,+∞)为单调递增函数,不存在最小值,故①错误;
②,∵f(2-x)=f(2+x),
∴f(4-x)=f(x),又f(x)为定义在R上周期为4的函数,
∴f(x)=f(4-x)=f(-x),
∴f(x)为偶函数,故②正确;
③,∵定义在R上的函数f(x)既是奇函数又是以2为周期的周期函数,
∴f(4)=f(0)=0;f(7)=f(8-1)=f(-1)=-f(1),
∴f(1)+f(4)+f(7)=f(1)+0-f(1)=0,故③正确;
④,∵f(x)=ax3+bx2+cx+d(a≠0),
∴f′(x)=3ax2+2bx+c(a≠0),
要使y=f(x)有极值,则方程3ax2+2bx+c=0(a≠0)有两异根,
∴△=4b2-12ac>0,即b2-3ac>0;
当a+b+c=0(a≠0)时,b=-(a+c),b2-3ac=(a+c)2-3ac=a2+c2-ac=(a-
)2+
c2>0,充分性成立,反之不然;
∴a+b+c=0是f(x)有极值的充分不必要条件,故④错误;
⑤,∵f(x)=x-sinx,
∴f′(x)=1-cosx≥0,
∴f(x)=x-sinx为R上的增函数,
又f(-x)=-x+sinx=-(x-sinx)=-f(x),
∴f(x)=x-sinx为R上的奇函数;
∴若a+b>0,即a>-b时,f(a)>f(-b=-f(b),
∴f(a)+f(b)>0,故⑤正确.
综上所述,正确的命题序号为:②③⑤.
故答案为:②③⑤
| a |
| x |
当a≤0时,在f(x)在(0,+∞)为单调递增函数,不存在最小值,故①错误;
②,∵f(2-x)=f(2+x),
∴f(4-x)=f(x),又f(x)为定义在R上周期为4的函数,
∴f(x)=f(4-x)=f(-x),
∴f(x)为偶函数,故②正确;
③,∵定义在R上的函数f(x)既是奇函数又是以2为周期的周期函数,
∴f(4)=f(0)=0;f(7)=f(8-1)=f(-1)=-f(1),
∴f(1)+f(4)+f(7)=f(1)+0-f(1)=0,故③正确;
④,∵f(x)=ax3+bx2+cx+d(a≠0),
∴f′(x)=3ax2+2bx+c(a≠0),
要使y=f(x)有极值,则方程3ax2+2bx+c=0(a≠0)有两异根,
∴△=4b2-12ac>0,即b2-3ac>0;
当a+b+c=0(a≠0)时,b=-(a+c),b2-3ac=(a+c)2-3ac=a2+c2-ac=(a-
| c |
| 2 |
| 3 |
| 4 |
∴a+b+c=0是f(x)有极值的充分不必要条件,故④错误;
⑤,∵f(x)=x-sinx,
∴f′(x)=1-cosx≥0,
∴f(x)=x-sinx为R上的增函数,
又f(-x)=-x+sinx=-(x-sinx)=-f(x),
∴f(x)=x-sinx为R上的奇函数;
∴若a+b>0,即a>-b时,f(a)>f(-b=-f(b),
∴f(a)+f(b)>0,故⑤正确.
综上所述,正确的命题序号为:②③⑤.
故答案为:②③⑤
点评:本题考查命题的真假判断与应用,主要考查函数的单调性、奇偶性、周期性的综合应用,考查导数法判定极值及充分必要条件概念及其应用,属于中档题.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
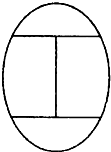 某校园有一椭圆型花坛,分成如图四块种花,现有4种不同颜色的花可供选择,要求每块地只能种一种颜色,且有公共边界的两块不能种同一种颜色,则不同的种植方法共有( )
某校园有一椭圆型花坛,分成如图四块种花,现有4种不同颜色的花可供选择,要求每块地只能种一种颜色,且有公共边界的两块不能种同一种颜色,则不同的种植方法共有( )| A、48种 | B、36种 |
| C、30种 | D、24种 |
极点与直角坐标系的原点重合,极轴与x轴非负半轴重合,曲线C的极坐标方程为ρ=2sinθ,直线l的参数方程为
(t为参数),直线l与曲线C交于A、B,则 线段AB的长等于( )
|
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
执行如图所示的程序框图,输出的S是( )


| A、10 | B、15 | C、20 | D、35 |
若x为实数,则函数y=x2+3x-5的最小值为( )
A、-
| ||
| B、-5 | ||
| C、0 | ||
| D、不存在 |