题目内容
19.在区间[0,1]上随机取两个实数a、b,则函数$f(x)=\frac{1}{2}{x^3}+ax-b$在区间[0,1]上有且只有一个零点的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
分析 由题意知本题是一个几何概型,根据所给的条件很容易做出试验发生包含的事件对应的面积,而满足条件的事件是函数f(x)=$\frac{1}{2}$x3+ax-b在区间[0,1]上有且仅有一个零点,求出导函数,看出函数是一个增函数,有零点等价于在自变量区间的两个端点处函数值符号相反,得到条件,做出面积,根据几何概型概率公式得到结果.
解答 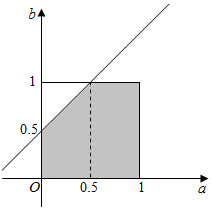 解:由题意知本题是一个几何概型,
解:由题意知本题是一个几何概型,
∵a∈[0,1],
∴f'(x)=1.5x2+a≥0,
∴f(x)是增函数,
若在[0,1]有且仅有一个零点,则f(0)•f(1)≤0,
∴-b•(0.5+a-b)≤0,
即b(0.5+a-b)≥0,
∴b≤a+0.5,
由线性规划内容知全部事件的面积为1×1=1,满足条件的面积为1-$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$=$\frac{7}{8}$,
∴概率P=$\frac{7}{8}$,
故选:D.
点评 本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.

练习册系列答案
相关题目
10.已知圆锥的全面积是底面积的3倍,那么这个圆锥的侧面积展开图扇形的圆心角为 ( )
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{6}$ | D. | π |
7.已知i为虚数单位,若(1+i) z=2i,则复数z=( )
| A. | 1-i | B. | 1+i | C. | 2-2i | D. | 2+2i |
4.若角α与角β终边相同,则一定有( )
| A. | α+β=180° | B. | α+β=0° | C. | α-β=k•360°,k∈Z | D. | α+β=k•360°,k∈Z |
8.已知命题p:?x∈R,sinx≥-1,则¬p( )
| A. | ?x0∈R,sinx0≤-1 | B. | ?x0∈R,sinx0<-1 | C. | ?x∈R,sinx≤-1 | D. | ?x∈R,sinx<-1 |
 为了解荆州中学学生健康状况,从去年高二年级体检表中抽取若干份,将他们的体重数据作为样本.将样本的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解荆州中学学生健康状况,从去年高二年级体检表中抽取若干份,将他们的体重数据作为样本.将样本的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12. 课本介绍过平面向量数量积运算的几何意义:$\overrightarrow a•\overrightarrow b$等于$\overrightarrow a$的长度$|{\overrightarrow a}|$与$\overrightarrow b$在$\overrightarrow a$方向上的投影$|{\overrightarrow b}|cos<\overrightarrow a,\overrightarrow b>$的乘积.运用几何意义,有时能得到更巧妙的解题思路.例如:边长为1的正六边形ABCDEF中,点P是正六边形内的一点(含边界),则$\overrightarrow{AP}•\overrightarrow{AB}$的取值范围是$[{-\frac{1}{2},\frac{3}{2}}]$.
课本介绍过平面向量数量积运算的几何意义:$\overrightarrow a•\overrightarrow b$等于$\overrightarrow a$的长度$|{\overrightarrow a}|$与$\overrightarrow b$在$\overrightarrow a$方向上的投影$|{\overrightarrow b}|cos<\overrightarrow a,\overrightarrow b>$的乘积.运用几何意义,有时能得到更巧妙的解题思路.例如:边长为1的正六边形ABCDEF中,点P是正六边形内的一点(含边界),则$\overrightarrow{AP}•\overrightarrow{AB}$的取值范围是$[{-\frac{1}{2},\frac{3}{2}}]$.