题目内容
7.已知i为虚数单位,若(1+i) z=2i,则复数z=( )| A. | 1-i | B. | 1+i | C. | 2-2i | D. | 2+2i |
分析 把已知的等式变形,利用复数代数形式的乘除运算化简得答案.
解答 解:由(1+i) z=2i,得$z=\frac{2i}{1+i}=\frac{2i(1-i)}{(1+i)(1-i)}=\frac{2+2i}{2}=1+i$,
故选:B.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
18.设三棱锥O-ABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,G是△ABC的重心,则$\overrightarrow{OG}$等于( )
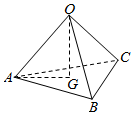

| A. | $\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$ | B. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$) | D. | $\frac{1}{3}$($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$) |
15.已知函数f(x)=sinx-cosx且f′(x)=2f(x),则tanx=( )
| A. | -3 | B. | 3 | C. | 1 | D. | -1 |
12.若函数$y={log_2}({x^2}-ax+3a)$在(2,+∞)上是单调增函数,则实数a的取值范围为( )
| A. | (-∞,4] | B. | (-∞,4) | C. | (-4,4] | D. | [-4,4] |
19.在区间[0,1]上随机取两个实数a、b,则函数$f(x)=\frac{1}{2}{x^3}+ax-b$在区间[0,1]上有且只有一个零点的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
16.命题“?x∈R,都有log2x>0成立”的否定为( )
| A. | ?x0∈R,使log2x0≤0成立 | B. | ?x0∈R,使log2x>0成立 | ||
| C. | ?x∈R,都有log2x≥0成立 | D. | ?x∈R,都有log2x>0成立 |
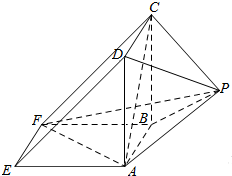 如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.