题目内容
10．已知圆锥的全面积是底面积的3倍，那么这个圆锥的侧面积展开图扇形的圆心角为 （ ）| A． | $\frac{π}{2}$ | B． | $\frac{2π}{3}$ | C． | $\frac{5π}{6}$ | D． | π |
分析 设圆锥的底面半径为r，母线长l，圆锥的侧面积展开图扇形的圆心角为θ，由已知可得l=2r，进而利用弧长公式，可得答案．
解答 解：设圆锥的底面半径为r，母线长l，圆锥的侧面积展开图扇形的圆心角为θ，
则πr（r+l）=3πr2，即l=2r，
则2πr=θl=2θr，
故θ=π，
故选：D．
点评 本题考查的知识是圆锥的表面积公式和弧长公式，难度不大，属于基础题．
练习册系列答案
相关题目
1．600°角是第（ ）象限的角．
| A． | 一 | B． | 二 | C． | 三 | D． | 四 |
18．设三棱锥O-ABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，G是△ABC的重心，则$\overrightarrow{OG}$等于（ ）
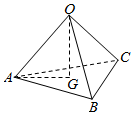
| A． | $\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$ | B． | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | C． | $\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$） | D． | $\frac{1}{3}$（$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$） |
15．已知函数f（x）=sinx-cosx且f′（x）=2f（x），则tanx=（ ）
| A． | -3 | B． | 3 | C． | 1 | D． | -1 |
19．在区间[0，1]上随机取两个实数a、b，则函数$f（x）=\frac{1}{2}{x^3}+ax-b$在区间[0，1]上有且只有一个零点的概率是（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{7}{8}$ |
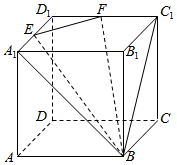如图，已知正方体ABCD-A1B1C1D1的边长为2，点E，F分别是A1D1，C1D1的中点．