题目内容
5.已知数列$\{a_n^{\;}\}$满足a1=2,${a_{n+1}}=2{a_n}+2\;\;(n∈{N^*})$.(1)求数列$\{a_n^{\;}\}$的通项公式an;
(2)若数列$\{b_n^{\;}\}满足b_n^{\;}={log_2}({a_n}+2)$,设Tn是数列$\{\frac{b_n}{{{a_n}+2}}\}$的前n项和,求证:${T_n}<\frac{3}{2}$.
分析 (1)通过对${a_{n+1}}=2{a_n}+2\;\;(n∈{N^*})$变形,整理可知数列{an+2}是以a1+2=4为首项,以2为公比的等比数列,进而计算可得结论;
(2)通过(1)可知$\frac{b_n}{{{a_n}+2}}=\frac{n+1}{{{2^{n+1}}}}$,进而利用错位相减法计算即得结论.
解答 (本题12分)
解:(1)∵${a_{n+1}}=2{a_n}+2\;\;(n∈{N^*})$,
∴an+1+2=2(an+2),即$\frac{{{a_{n+1}}+2}}{{{a_n}+2}}=2$…(3分)
又a2=2a1+2=6,即$\frac{{{a_2}+2}}{{{a_1}+2}}=2$也成立,
∴{an+2}是以a1+2=4为首项,以2为公比的等比数列…(5分)
∴${a_n}+2=4•{2^{n-1}}$,即${a_n}=4•{2^{n-1}}-2={2^{n+1}}-2$…(6分)
(2)由$b_n^{\;}={log_2}({a_n}+2)={log_2}{2^{n+1}}=n+1$得:$\frac{b_n}{{{a_n}+2}}=\frac{n+1}{{{2^{n+1}}}}$…(8分)
则 ${T_n}=\frac{2}{2^2}+\frac{3}{2^3}+\frac{4}{2^4}+…+\frac{n+1}{{{2^{n+1}}}}$③
$\frac{1}{2}{T_n}=\frac{2}{2^3}+\frac{3}{2^4}+\frac{4}{2^5}+…+\frac{n+1}{{{2^{n+2}}}}$④…(9分)
③-④得:$\frac{1}{2}{T_n}=\frac{2}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+…+\frac{1}{{{2^{n+1}}}}-\frac{n+1}{{{2^{n+2}}}}$
=$\frac{1}{4}+(\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+…+\frac{1}{{{2^{n+1}}}})-\frac{n+1}{{{2^{n+2}}}}$
=$\frac{1}{4}+\frac{{\frac{1}{4}(1-\frac{1}{2^n})}}{{1-\frac{1}{2}}}-\frac{n+1}{{{2^{n+2}}}}=\frac{3}{4}-\frac{n+3}{{{2^{n+2}}}}$…11分
所以${T_n}=\frac{3}{2}-\frac{n+3}{{{2^{n+1}}}}<\frac{3}{2}$…(12分)
点评 本题考查数列的通项及前n项和,考查运算求解能力,利用构造法是解决本题的关键,注意解题方法的积累,属于中档题.

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | f(x)=2sin(x+$\frac{π}{6}$) | B. | f(x)=2sin(x+$\frac{π}{3}$) | C. | f(x)=2sin(2x+$\frac{π}{6}$) | D. | f(x)=2sin(2x+$\frac{π}{3}$) |
| A. | x2-$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | ||
| C. | x2-$\frac{{y}^{2}}{2}$=1或y2-$\frac{{x}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-y2=1或$\frac{{y}^{2}}{2}$-x2=1 |
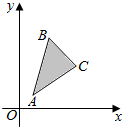 给出平面区域如图所示,其中A(1,1),B(2,5),C(4,3)若使目标函数z=ax-y仅在点C处取得最大值,则a的取值范围是$({\frac{2}{3},+∞})$.
给出平面区域如图所示,其中A(1,1),B(2,5),C(4,3)若使目标函数z=ax-y仅在点C处取得最大值,则a的取值范围是$({\frac{2}{3},+∞})$.