题目内容
用0，1，…，9，这十个数字，可以组成多少个三位整数？无重复数字的三位整数？小于500的无重复数字的三位整数？
考点：计数原理的应用
专题：应用题,排列组合
分析：（1）因为百位不能是0，可以有重复数字，所以可以组成9×10×10=900个三位数；
（2）因为0不能做百位，所以有9种方法；再确定十位数字，有除了百位数外的9个；最后确定个位数字有除了百位和十位数之外的8个．利用乘法原理，可得没有重复数字的三位数的个数；
（3）百位应小于5且不为0有4种取法；十位有9种取法，个位有8种取法，利用乘法原理，可得小于500的无重复数字的三位数的个数．
（2）因为0不能做百位，所以有9种方法；再确定十位数字，有除了百位数外的9个；最后确定个位数字有除了百位和十位数之外的8个．利用乘法原理，可得没有重复数字的三位数的个数；
（3）百位应小于5且不为0有4种取法；十位有9种取法，个位有8种取法，利用乘法原理，可得小于500的无重复数字的三位数的个数．
解答：
解：（1）因为百位不能是0，可以有重复数字，所以可以组成9×10×10=900个三位数；
（2）因为0不能做百位，所以有9种方法；再确定十位数字，有除了百位数外的9个；最后确定个位数字有除了百位和十位数之外的8个．所以能组成9×9×8=648个没有重复数字的三位数
（3）百位应小于5且不为0有4种取法；十位有9种取法，个位有8种取法，故能组成4×9×8=288个小于500的无重复数字的三位数
（2）因为0不能做百位，所以有9种方法；再确定十位数字，有除了百位数外的9个；最后确定个位数字有除了百位和十位数之外的8个．所以能组成9×9×8=648个没有重复数字的三位数
（3）百位应小于5且不为0有4种取法；十位有9种取法，个位有8种取法，故能组成4×9×8=288个小于500的无重复数字的三位数
点评：本题是考查排列组合问题，是一个综合题，同学们注意分析问题，加以比较，争取做到举一反三．
练习册系列答案
阅读快车系列答案
相关题目
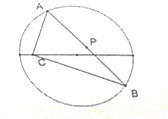已知x2+y2=a2，定点C（c，0）．（a＞0，c≠a）．AB为圆上的动点∠ACB=90°．求AB中点P的轨迹方程．
某超市对某商品开展为期两天的抽奖促销活动，第一天的活动方案为：顾客转动如图所示圆盘，当指针指向阴影部分（图中四个阴影部分均为扇形，且每个扇形圆心角均为15°，边界忽略不计）即为中奖．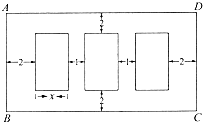
某公司因业务发展需要，准备印制如图所示的宣传彩页，宣传彩页有三幅大小相同的三个画面组成，每个画面的面积都是200cm2，这三个画面中都要绘制半径为5cm的圆形图案，为美观起见，每两个画面之间要留1cm的空白，三幅画周围要留2cm页边距，如图，设一边长x，所选用的彩页纸张面积为S