题目内容
20.设F1(-1,0),F2(1,0)是椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,P为E的上顶点,若$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=2,则a=( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 4 |
分析 由已知得P(0,b),$\overrightarrow{P{F}_{1}}$=(-1,-b),$\overrightarrow{P{F}_{2}}$=(1,-b),从而$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=b2-1=2,由此利用椭圆性质能求出a.
解答 解:∵F1(-1,0),F2(1,0)是椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,P为E的上顶点,
∴P(0,b),$\overrightarrow{P{F}_{1}}$=(-1,-b),$\overrightarrow{P{F}_{2}}$=(1,-b),
∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=2,
∴$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=b2-1=2,
解得b2=3,∴a2=3+1=4,
解得a=2.
故选:B.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
8.已知曲线f(x)=ex-ax在点(0,f(0))处的切线方程为3x+y+b=0,则下列不等式恒成立的是( )
| A. | f(x)≥2-4ln2 | B. | f(x)≤2-4ln2 | C. | f(x)≥4-8ln2 | D. | f(x)≤4-8ln2 |
15.复数$\frac{2}{(1-i)i}$(i为复数单位)的共轭复数为( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
12.若集合A={x|x+2<0},B={x|-4<x<3},则集合A∩B为( )
| A. | {x|x<3} | B. | {x|-4<x<-2} | C. | {x|-4<x<2} | D. | {x|-2<x<3} |
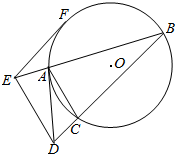 如图所示,△ABC内接于⊙O,直线AD与⊙O相切于点A,交BC的延长线于点D,过点D作DE∥CA交BA的延长线于点E.
如图所示,△ABC内接于⊙O,直线AD与⊙O相切于点A,交BC的延长线于点D,过点D作DE∥CA交BA的延长线于点E.