题目内容
18．已知实数x，y满足条件$\left\{\begin{array}{l}x-y≥-1\\ x+y≤4\\ x-2y≤0\end{array}\right.$，若使z=ax+y取到最大值的最优解有无数个，则实数a=（ ）| A． | -1 | B． | 1 | C． | ±1 | D． | $-\frac{1}{2}$ |
分析 不等式组表示的平面区域，z=ax+y的几何意义是直线y=-ax+z的纵截距，利用z=ax+y取得最大值时的最优解（x，y）有无数个，可得y=-ax+z与直线y+x+1=0平行，故可求a的值．
解答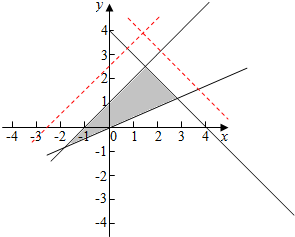 
解：不等式组$\left\{\begin{array}{l}x-y≥-1\\ x+y≤4\\ x-2y≤0\end{array}\right.$表示的平面区域如图，z=ax+y的几何意义是直线y=-ax+z的纵截距，
∵z=ax+y取得最大值时的最优解（x，y）有无数个，
∴y=-ax+z与直线y+x-4=0或x-y+1=0平行
∴a=±1
故选：C．
点评 本题考查线性规划知识，考查最优解，考查数形结合的数学思想．
练习册系列答案
相关题目
8．已知曲线f（x）=ex-ax在点（0，f（0））处的切线方程为3x+y+b=0，则下列不等式恒成立的是（ ）
| A． | f（x）≥2-4ln2 | B． | f（x）≤2-4ln2 | C． | f（x）≥4-8ln2 | D． | f（x）≤4-8ln2 |
13．己知函数f（x）=sinx+$\sqrt{3}$cosx（x∈R），先将y=f（x）的图象上所有点的横坐标缩短到原来的$\frac{1}{2}$倍（纵坐标不变），再将得到的图象上所有点向右平行移动θ（θ＞0）个单位长度，得到的图象关于直线x=$\frac{3π}{4}$对称，则θ的最小值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{12}$ | D． | $\frac{2π}{3}$ |