题目内容
2.已知函数f(x)=x2+ax+1,(Ⅰ)设g(x)=(2x-3)f(x),若y=g(x)与x轴恰有两个不同的交点,试求a的取值集合;
(Ⅱ)求函数y=|f(x)|在[0,1]上的最大值.
分析 (Ⅰ)分类讨论,从而由f(x)=0恰有一解及f(x)=0有两个不同的解求得;
(Ⅱ)分类讨论,从而确定二次函数的单调性及最值,从而确定函数y=|f(x)|在[0,1]上的最大值.
解答 解:(Ⅰ)(1)若f(x)=0恰有一解,且解不为$\frac{3}{2}$,
即a2-4=0,解得a=±2;
(2)若f(x)=0有两个不同的解,且其中一个解为$\frac{3}{2}$,
代入得$\frac{9}{4}+\frac{3}{2}a+1=0$,
故$a=-\frac{13}{6}$;
综上所述,a的取值集合为$\{-\frac{13}{6},-2,2\}$.
(Ⅱ)(1)若$-\frac{a}{2}≤0$,即a≥0时,
函数y=|f(x)|在[0,1]上单调递增,
故ymax=f(1)=2+a;
(2)若$0<-\frac{a}{2}<1$,即-2<a<0时,
此时△=a2-4<0,且f(x)的图象的对称轴在(0,1)上,且开口向上;
故${y_{max}}=max\{f(0),f(1)\}=max\{1,a+2\}=\left\{{\begin{array}{l}{a+2}&{a≥-1}\\ 1&{a<-1}\end{array}}\right.$,
(3)若$-\frac{a}{2}≥1$,即a≤-2时,
此时f(1)=2+a≤0,
${y_{max}}=max\{f(0),-f(1)\}=max\{1,-a-2\}=\left\{{\begin{array}{l}1&{a≥-3}\\{-a-2}&{a<-3}\end{array}}\right.$,
综上所述,${y_{max}}=\left\{{\begin{array}{l}{a+2}&{a≥-1}\\ 1&{-3≤a<-1}\\{-a-2}&{a<-3}\end{array}}\right.$.
点评 本题考查了分类讨论的思想应用及数形结合的思想应用,同时考查了二次函数的性质应用.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案| A. | {x|x<3} | B. | {x|-4<x<-2} | C. | {x|-4<x<2} | D. | {x|-2<x<3} |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{2π}{3}$ |
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
| A. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| B. | “a=3”是“函数f(x)=logax在定义域上为增函数”的充分不必要条件 | |
| C. | 若命题p:?n∈N,3n>100,则¬p:?n∈N,3n≤100 | |
| D. | 命题“?x∈(-∞,0),3x<5x”是真命题 |
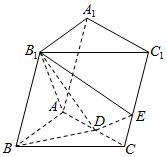 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.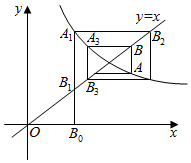 如图所示,折线B0A1B2A2B3A3…中线段分别平行于x轴或y轴,A1,A2,…,An…这些点在函数y=$\frac{2}{x-1}$(x>1)图象上,B1,B2…Bn…这些点在直线y=x上,设点An的纵坐标为yn.
如图所示,折线B0A1B2A2B3A3…中线段分别平行于x轴或y轴,A1,A2,…,An…这些点在函数y=$\frac{2}{x-1}$(x>1)图象上,B1,B2…Bn…这些点在直线y=x上,设点An的纵坐标为yn.