题目内容
1．函数$f（x）=sinx-\sqrt{3}cosx，\;x∈[0，\frac{π}{2}]$的值域是[-$\sqrt{3}$，1]．分析 利用辅助角公式化简函数的解析式，再利用正弦函数的定义域和值域得出结论．
解答 解：∵x∈[0，$\frac{π}{2}$]，x-$\frac{π}{3}$∈[-$\frac{π}{3}$，$\frac{π}{6}$]，
∴f（x）=sinx-$\sqrt{3}$cosx=2sin（x-$\frac{π}{3}$）∈[-$\sqrt{3}$，1]，
故答案为：[-$\sqrt{3}$，1]．
点评 本题主要考查辅助角公式，正弦函数的定义域和值域，属于基础题．
练习册系列答案
相关题目
12．若集合A={x|x+2＜0}，B={x|-4＜x＜3}，则集合A∩B为（ ）
| A． | {x|x＜3} | B． | {x|-4＜x＜-2} | C． | {x|-4＜x＜2} | D． | {x|-2＜x＜3} |
13．己知函数f（x）=sinx+$\sqrt{3}$cosx（x∈R），先将y=f（x）的图象上所有点的横坐标缩短到原来的$\frac{1}{2}$倍（纵坐标不变），再将得到的图象上所有点向右平行移动θ（θ＞0）个单位长度，得到的图象关于直线x=$\frac{3π}{4}$对称，则θ的最小值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{12}$ | D． | $\frac{2π}{3}$ |
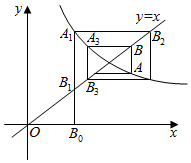如图所示，折线B0A1B2A2B3A3…中线段分别平行于x轴或y轴，A1，A2，…，An…这些点在函数y=$\frac{2}{x-1}$（x＞1）图象上，B1，B2…Bn…这些点在直线y=x上，设点An的纵坐标为yn．