题目内容
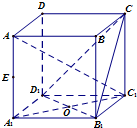如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点．（1）求证：AC1⊥平面B1D1C；
（2）过E构造一条线段与平面B1D1C垂直，并证明你的结论．
考点：直线与平面垂直的判定,棱柱的结构特征
专题：证明题,探究型,空间位置关系与距离
分析：（1）先证明B1D1⊥平面AA1C1，即可证B1D1⊥AC1，同理可证AC1⊥B1C，从而证明AC1⊥B1D1C．
（2）连结EO，此线段与平面B1D1C垂直，由E是AA1的中点，O是A1C1的中点，得EO∥AC1，由AC1⊥平面B1D1C，可证EO⊥平面B1D1C．
（2）连结EO，此线段与平面B1D1C垂直，由E是AA1的中点，O是A1C1的中点，得EO∥AC1，由AC1⊥平面B1D1C，可证EO⊥平面B1D1C．
解答：
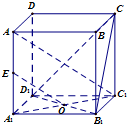证明：（1）∵AA1⊥平面A1B1C1D1，∴AA1⊥B1D1．
∵A1C1⊥B1D1，且AA1∩A1C1=A1，
∴B1D1⊥平面AA1C1，∴B1D1⊥AC1．
同理，AC1⊥B1C，∴AC1⊥B1D1C．
（2）连结EO，此线段与平面B1D1C垂直．
∵E是AA1的中点，O是A1C1的中点，∴EO∥AC1．
∵AC1⊥平面B1D1C，∴EO⊥平面B1D1C．
证明：（1）∵AA1⊥平面A1B1C1D1，∴AA1⊥B1D1．∵A1C1⊥B1D1，且AA1∩A1C1=A1，
∴B1D1⊥平面AA1C1，∴B1D1⊥AC1．
同理，AC1⊥B1C，∴AC1⊥B1D1C．
（2）连结EO，此线段与平面B1D1C垂直．
∵E是AA1的中点，O是A1C1的中点，∴EO∥AC1．
∵AC1⊥平面B1D1C，∴EO⊥平面B1D1C．
点评：本题主要考察了直线与平面垂直的判定，连结EO，探究此线段与平面B1D1C垂直是解题的关键，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知集合M=x={x|-3＜x＜1}，N={x|x≤3}，则集合{x|x≤-3或x≥1}=（ ）
| A、M∩N |
| B、M∪N |
| C、∁M（M∩N） |
| D、∁M（M∪N） |
下列判断正确的是（ ）
| A、若一条直线l与平面α平行，则直线l与平面α内所有直线平行 |
| B、若两条直线l1，l2都与平面α平行，则l1∥l2 |
| C、若一条直线与两个平面α，β都垂直，则平面α∥平面β |
| D、若一条直线与两个平面α，β都平行，则平面α∥平面β |