题目内容
对于函数f(x)=
给出下列四个命题:①该函数是以π为最小正周期的周期函数;②当且仅当x=π+kπ(k∈Z)时,该函数取得最小值-1;③该函数的图象关于x=
+2kπ(k∈Z)对称;④当且仅当2kπ<x<
+2kπ(k∈Z)时,0<f(x)≤
.其中正确命题的序号是( )
|
| 5π |
| 4 |
| π |
| 2 |
| ||
| 2 |
| A、①② | B、①③ | C、②④ | D、③④ |
考点:命题的真假判断与应用
专题:三角函数的图像与性质
分析:由题意作出此分段函数的图象,由图象研究该函数的性质,依据这些性质判断四个命题的真假,此函数取自变量相同时函数值小的那一个,由此可顺利作出函数图象.
解答:
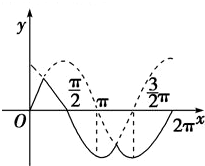 解:由题意函数f(x)=
解:由题意函数f(x)=
,画出f(x)在x∈[0,2π]上的图象.
由图象知,函数f(x)的最小正周期为2π,故①错误;
在x=π+2kπ(k∈Z)和x=
+2kπ(k∈Z)时,该函数都取得最小值-1,故②错误,
由图象知,函数图象关于直线x=
+2kπ(k∈Z)对称,故③正确
在2kπ<x<
+2kπ(k∈Z)时,0<f(x)≤
,故④正确.
故正确命题的序号是:③④,
故选:D
 解:由题意函数f(x)=
解:由题意函数f(x)=
|
由图象知,函数f(x)的最小正周期为2π,故①错误;
在x=π+2kπ(k∈Z)和x=
| 3π |
| 2 |
由图象知,函数图象关于直线x=
| 5π |
| 4 |
在2kπ<x<
| π |
| 2 |
| ||
| 2 |
故正确命题的序号是:③④,
故选:D
点评:本题考点是三角函数的最值,本题是函数图象的运用,由函数的图象研究函数的性质,并以由图象研究出的结论判断和函数有关的命题的真假.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列说法错误的是( )
| A、如果命题“¬p”与命题“p∨q”都是真命题,那么命题q一定是真命题 | ||
| B、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | ||
| C、若命题p:?x0∈R,x02+2x0-3<0,则?p:?x∈R,x2+2x-3≥0 | ||
D、“sinθ=
|
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为3x+4y=0,则双曲线离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线y=b(b>0)与曲线f(x)=sinx在y轴右侧依次的三个交点的横坐标x1,x2,x3成等比数列,则b的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
若P(A)=
,P(B|A)=
,则P(AB)等于( )
| 9 |
| 10 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
“m=2”是“直线3x+(m+1)y-(m-7)=0与直线mx+2y+3m=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=
如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=