题目内容
19.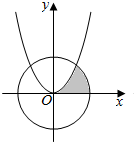 若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )
若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )| A. | $\frac{1}{8}$-$\frac{1}{12π}$ | B. | $\frac{1}{8}$+$\frac{1}{12π}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{12π}$ |
分析 首先通过二项式的展开式常数求出a,然后利用定积分求出封闭图形的面积,再由几何概型的几何意义求出概率.
解答 解:因为(x2+$\frac{a}{2x}$)6展开式的常数项是15,
所以${C}_{6}^{4}(\frac{a}{2})^{4}$=15,解得a=2,
所以曲线y=x2和圆x2+y2=2的在第一象限的交点为(1,1)
所以阴影部分的面积为$\frac{π}{4}$-${∫}_{0}^{1}{(x-x}^{2})dx$=$\frac{π}{4}$-($\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}$)|${\;}_{0}^{1}$=$\frac{π}{4}-\frac{1}{6}$.
所以石子恰好落在阴影部分的概率$\frac{\frac{π}{4}-\frac{1}{6}}{2π}=\frac{1}{8}-\frac{1}{12π}$;
故选:A
点评 本题考查了二项式定理以及定积分求阴影部分的面积以及几何概型的概率求法;属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.圆x2+y2-2x+4y+1=0的半径为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
14.若角α与角β的终边关于y轴对称,则( )
| A. | α+β=π+kπ(k∈Z) | B. | α+β=π+2kπ(k∈Z) | C. | $α+β=\frac{π}{2}+kπ(k∈Z)$ | D. | $α+β=\frac{π}{2}+2kπ(k∈Z)$ |
4.函数f(x)=$\sqrt{3-x}$-2lg(x+1)的定义域为( )
| A. | (-1,3] | B. | (-∞,3] | C. | [3,+∞) | D. | (-1,+∞) |
11.定义在R上的函数f(x)=$\left\{\begin{array}{l}{(1-2a)x+\frac{1}{2},x∈(-∞,1]}\\{alo{g}_{a}x,x∈(1,+∞)}\end{array}\right.$(其中a>0,且a≠1),对于任意x1≠x2都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,则实数a的取值范围是( )
| A. | [$\frac{3}{4}$,1) | B. | ($\frac{1}{2}$,$\frac{3}{4}$] | C. | ($\frac{1}{2}$,$\frac{3}{4}$) | D. | ($\frac{1}{2}$,1) |
8.如果在一次实验中,测得数对(x,y)的四组数值分别是A(1,2),B(2,3),C(3,6),D(4,7),则y与x之间的回归直线方程是( )
| A. | $\widehat{y}$=x+1.9 | B. | $\widehat{y}$=1.8x | C. | $\widehat{y}$=0.95x+1.04 | D. | $\widehat{y}$=1.05x-0.9 |
9.设函数y=x3与y=2x+1的图象的交点为(x0,y0),则x0所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |