题目内容
5.已知抛物线y2=4x与直线y=x-1交于A,B两点.(I)求该抛物线的焦点坐标及准线方程;
(Ⅱ)求线段AB的长.
分析 (Ⅰ)根据抛物线标准方程便可得到p=2,从而可以得出焦点坐标和准线方程;
(Ⅱ)联立抛物线和直线方程,消去y可得到x2-6x+1=0,可设A(x1,y1),B(x2,y2),从而有x1+x2=6,可看出直线y=x-1过焦点,从而根据抛物线定义可得到|AB|=|AF|+|BF|=x1+x2+2,这样便可求得线段AB的长.
解答 解:(Ⅰ)抛物线的焦点坐标为(1,0);
准线方程为 x=-1;
(Ⅱ)由方程组 $\left\{\begin{array}{l}{y^2}=4x\\ y=x-1\end{array}\right.$得:
x2-6x+1=0,设A(x1,y1),B(x2,y2),则:x1+x2=6;
如图,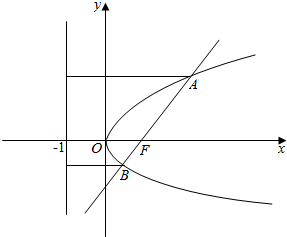
直线y=x-1过焦点,A,B到准线的距离分别为d1,d2;
由抛物线定义可知|AB|=|AF|+|BF|=d1+d2=x1+x2+2=8;
即线段AB的长为8.
点评 考查抛物线的标准方程,抛物线的焦点和准线,韦达定理,以及抛物线的定义.

练习册系列答案
相关题目
18.{an}是公差d=3等差数列,若a10=28,an=2008,则n等于( )
| A. | 668 | B. | 669 | C. | 670 | D. | 671 |
14.若角α与角β的终边关于y轴对称,则( )
| A. | α+β=π+kπ(k∈Z) | B. | α+β=π+2kπ(k∈Z) | C. | $α+β=\frac{π}{2}+kπ(k∈Z)$ | D. | $α+β=\frac{π}{2}+2kπ(k∈Z)$ |