题目内容
10.函数f(x)=$\frac{1}{2}$x2-lnx的单调递减区间为( )| A. | (-1,1) | B. | (-∞,1) | C. | (1,+∞) | D. | (0,1) |
分析 求出函数的定义域,利用导函数的符号列出不等式求解即可.
解答 解:函数f(x)=$\frac{1}{2}$x2-lnx的定义域为:{x|x>0}.
函数f(x)=$\frac{1}{2}$x2-lnx的导函数为:f′(x)=x-$\frac{1}{x}$,
令x-$\frac{1}{x}$<0并且x>0,解得0<x<1.
函数f(x)=$\frac{1}{2}$x2-lnx的单调递减区间为(0,1).
故选:D.
点评 本题考查函数的单调性的求法,函数的导数的应用,注意函数的定义域.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若${(1+i)^2}+|2i|=\bar z$,其中z=a+bi(a,b∈R,i为虚数单位),则直线bx-ay+a=0的斜率为( )
| A. | -2 | B. | -1 | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
18.在三棱锥P-ABC中,$PA=PB=PC=\sqrt{6}$,AC=AB=2,且AC⊥AB,则该三棱锥外接球的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 9π |
15.在同一平面直角坐标系中,函数y=g(x)的图象与y=lnx的图象关于直线y=x对称,而函数y=f(x)的图象与y=g(x)的图象关于y轴对称,若f(-m)=e2,则m的值是( )
| A. | -e | B. | 2 | C. | -2 | D. | $\frac{1}{e}$ |

 .
. ,且
,且 对任意
对任意 恒成立, 求实数
恒成立, 求实数 的取值范围;
的取值范围; ,且关于
,且关于 的不等式
的不等式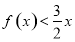 有解, 求实数
有解, 求实数 满足约束条件
满足约束条件 ,则
,则 的最小值是( )
的最小值是( ) D.3
D.3