题目内容
已知某校在一次考试中,5名学生的数学和地理成绩如表:
(1)根据上表,利用最小二乘法,求出y关于x的线性回归方程
=
x+
(其中
=0.36);
(2)利用(1)中的线性回归方程,试估计数学90分的同学的地理成绩(四舍五入到整数);
(3)若从五人中选2人参加数学竞赛,其中1、2号不同时参加的概率是多少?
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学成绩x | 80 | 75 | 70 | 65 | 60 |
| 地理成绩y | 70 | 66 | 68 | 64 | 62 |
| ∧ |
| y |
| ∧ |
| b |
| ∧ |
| a |
| ∧ |
| b |
(2)利用(1)中的线性回归方程,试估计数学90分的同学的地理成绩(四舍五入到整数);
(3)若从五人中选2人参加数学竞赛,其中1、2号不同时参加的概率是多少?
考点:线性回归方程,古典概型及其概率计算公式
专题:概率与统计
分析:(1)求出样本中心,代入回归直线方程,即可求出
,然后求解线性回归方程
=
x+
;
(2)利用(1)中的线性回归方程,代入x=90,求出y的值,即可得到这个同学的地理成绩.
(3)求出所有基本事件的总数,找出1、2号不同时参加的数目,即可求解概率.
| ∧ |
| a |
| ∧ |
| y |
| ∧ |
| b |
| ∧ |
| a |
(2)利用(1)中的线性回归方程,代入x=90,求出y的值,即可得到这个同学的地理成绩.
(3)求出所有基本事件的总数,找出1、2号不同时参加的数目,即可求解概率.
解答:
解:(1)
=
(80+75+70+65+60)=70
=
(70+66+68+64+62)=66
∴
=
-
=40.8
∴y关于x的线性回归方程为
=0.36
+40.8
(2)若x=90
则y=0.36×90+40.8≈73
即数学9(0分)的同学的地理成绩估计为7(3分)
(3)五人中选两人的不同选法有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种不同选法.
其中1、2号不同时参加的有九种,
∴两个不同时参加的概率P=
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
∴
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
∴y关于x的线性回归方程为
| ? |
| y |
| ? |
| x |
(2)若x=90
则y=0.36×90+40.8≈73
即数学9(0分)的同学的地理成绩估计为7(3分)
(3)五人中选两人的不同选法有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种不同选法.
其中1、2号不同时参加的有九种,
∴两个不同时参加的概率P=
| 9 |
| 10 |
点评:本题考查回归直线方程的求法,古典概型的应用,基本知识的考查.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
已知全集U={x∈Z|x2-9x+8<0},M={3,5,6},N={x|x2-9x+20=0},则集合{2,7}为( )
| A、M∪N |
| B、M∩N |
| C、∁U(M∪N) |
| D、∁U(M∩N) |
已知实数a,b,c满足
,则a+b的取值范围是( )
|
A、(
| ||||
B、(1,
| ||||
C、(1,
| ||||
D、(-
|
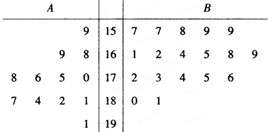 某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成茎叶图如图(单位:cm)若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成茎叶图如图(单位:cm)若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.