题目内容
18．某开发公司要生产若干件新产品，需要精加工后，才能投放市场，现有甲、乙两个加工厂都想加工这批产品．已知甲、乙两个工厂每天分别能加工这种产品16件和24件，且知单独加工这批产品甲比乙要多用20天，又知若由甲单独做，公司需付甲厂每天费用180元，若由乙厂单独做，公司需付乙厂每天费用220元．（1）求这批产品共有多少件？
（2）在加工过程中，公司需另派一名工程师到厂进行技术指导，并由公司为其提供每天10元的午餐补助费，公司制定产品加工方案如下：可由一个工厂单独加工完成；也可以由两个厂合作完成，请你帮助公司从所有可供选择的方案中，选择一种最省钱的加工方案．
分析 （1）设这批产品共有x件，根据题意构造方程$\frac{x}{16}$-$\frac{x}{24}$=20，解得答案；
（2）分别讨论出由甲厂单独加工，由乙厂单独加工，由两厂合作加工的费用，比较后，可得答案．
解答 解：（1）设这批产品共有x件，
则$\frac{x}{16}$-$\frac{x}{24}$=20，
解得：x=960，
即这批产品共有960件；
（2）由甲厂单独加工：需要耗时$\frac{960}{16}$=60天，需要费用为：60×（180+10）=11400元；
由乙厂单独加工：需要耗时$\frac{960}{24}$=40天，需要费用为：40×（220+10）=9200元；
由两厂合作加工：需要耗时$\frac{960}{24+16}$=24天，需要费用为：24×（220+10+180+10）=10080元；
故有乙厂单独加工最省钱．
点评 本题考查的知识点是根据实际选择函数模型，一元一次方程的应用，难度中档．
练习册系列答案
三点一测快乐周计划系列答案
相关题目
9．在△ABC中，a2+b2-c2=ab，则cosC=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $-\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
6．函数y=loga（x+1）（a＞0且a≠1）的图象恒过点为（ ）
| A． | （1，0） | B． | （0，1） | C． | （-1，0） | D． | （0，0） |
13．若函数f（x）同时满足以下三个性质：①f（x）的最小正周期为π；②对任意的x∈R，都有f（x-$\frac{π}{4}$）+f（-x）=0；③f（x）在（$\frac{π}{4}$，$\frac{π}{2}$）上是减函数，则f（x）的解析式可能是（ ）
| A． | f（x）=sin2x+cos2x | B． | f（x）=sin2x | C． | f（x）=tan（x+$\frac{π}{8}$） | D． | f（x）=cos2x |
3．已知数列{an}中，a1=1，an+1=an（1-nan+1），则数列{an}的通项公式为（ ）
| A． | an=$\frac{{n}^{2}-n+2}{2}$ | B． | an=$\frac{{n}^{2}-n+1}{2}$ | C． | an=$\frac{2}{{n}^{2}-n+1}$ | D． | an=$\frac{2}{{n}^{2}-n+2}$ |
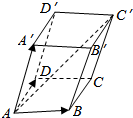在平行六面体（底面是平行四边形的四棱柱）ABCD-A′B′C′D′中，分别标出$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AA′}$，$\overrightarrow{AB}$+$\overrightarrow{AA′}$+$\overrightarrow{AD}$表示的向量．从中你能体会向量加法运算的交换律及结合律吗？一般地，三个不共面的向量的和与这三个向量有什么关系．