题目内容
20.设函数f(x)=sin(2x+$\frac{π}{4}$)(x∈[0,$\frac{9π}{8}$]),若方程f(x)=a恰好有三个根,分别为x1,x2,x3(x1<x2<x3),则x1+x2+x3的取值范围是( )| A. | [$\frac{9π}{8}$,$\frac{5π}{4}$) | B. | [$\frac{5π}{4}$,$\frac{11π}{8}$) | C. | [$\frac{3π}{2}$,$\frac{13π}{8}$) | D. | [$\frac{7π}{4}$,$\frac{15π}{8}$) |
分析 由x∈[0,$\frac{9π}{8}$]求出2x+$\frac{π}{4}$的范围,由正弦函数的图象画出函数的大致图象,由函数的图象,以及正弦图象的对称轴求出x1+x2的值,判断出x3的范围,即可求出x1+x2+x3的取值范围.
解答 解:由题意x∈[0,$\frac{9π}{8}$],则2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{2}$],
画出函数的大致图象:
由图得,当$\frac{\sqrt{2}}{2}≤a<1$ 时,方程f(x)=a恰好有三个根,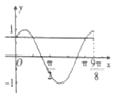
由2x+$\frac{π}{4}$=$\frac{π}{2}$得x=$\frac{π}{8}$,由2x+$\frac{π}{4}$=$\frac{3π}{2}$得x=$\frac{5π}{8}$,
由图知,点(x1,0)与点(x2,0)关于直线$x=\frac{π}{8}$对称,
点(x2,0)与点(x3,0)关于直线$x=\frac{5π}{8}$对称,
∴x1+x2=$\frac{π}{4}$,π≤x3<$\frac{9π}{8}$,则$\frac{5π}{4}≤$ x1+x2+x3<$\frac{11π}{8}$,
即x1+x2+x3的取值范围是$[\frac{5π}{4},\frac{11π}{8})$,
故选B.
点评 本题考查正弦函数的图象,以及正弦函数图象对称性的应用,考查整体思想,数形结合思想.

练习册系列答案
相关题目
10.设α,β是两个不同的平面,l是一条直线,以下命题正确的是( )
| A. | 若l⊥α,α⊥β,则 l?β | B. | 若l∥α,α∥β,则 l?β | ||
| C. | 若l⊥α,α∥β,则 l⊥β | D. | 若l∥α,α⊥β,则l⊥β |
8.在高中学习过程中,同学们经常这样说“如果物理成绩好,那么学习数学就没什么问题”某班针对“高中生物理对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论,现从该班随机抽取5名学生在一次考试中的物理和数学成绩,如表:
(1)求数学y成绩关于物理成绩x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$(b精确到0.1),若某位学生的物理成绩为80分时,预测他的物理成绩.
(2)要从抽取的这五位学生中随机选出三位参加一项知识竞赛,以X表示选中的学生的数学成绩高于100分的人数,求随机变量X的分布列及数学期望.
(参考公式:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}n\stackrel{-2}{x}}$,$\stackrel{∧}{a}$=$\overline{y}$b$\overline{x}$,)参考数据:902+852+742+682+632=29394
90×130+85×125+74×110+68×95+63×90=42595.
| 编号 成绩 | 1 | 2 | 3 | 4 | 5 |
| 物理(x) | 90 | 85 | 74 | 68 | 63 |
| 数学(y) | 130 | 125 | 110 | 95 | 90 |
(2)要从抽取的这五位学生中随机选出三位参加一项知识竞赛,以X表示选中的学生的数学成绩高于100分的人数,求随机变量X的分布列及数学期望.
(参考公式:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}n\stackrel{-2}{x}}$,$\stackrel{∧}{a}$=$\overline{y}$b$\overline{x}$,)参考数据:902+852+742+682+632=29394
90×130+85×125+74×110+68×95+63×90=42595.
5.已知集合A={x|x(x-2)=0},B={x∈Z|x2≤1},则A∪B等于( )
| A. | {-2,-1,0,1} | B. | {-1,0,1,2} | C. | [-2,2] | D. | {0,2} |
16.若幂函数f(x)=xm-1在(0,+∞)上是增函数,则( )
| A. | m>1 | B. | m<1 | C. | m=1 | D. | 不能确定 |