题目内容
15.平面内到定点F(0,1)和定直线l:y=-1的距离之和等于4的动点的轨迹为曲线C.关于曲线C的几何性质,给出下列三个结论:①曲线C关于y轴对称;
②若点P(x,y)在曲线C上,则|y|≤2;
③若点P在曲线C上,则1≤|PF|≤4.
其中,所有正确结论的序号是①②③.
分析 设出曲线上的点的坐标,求出曲线方程,画出图象,即可判断选项的正误.
解答 解:设P(x,y)是曲线C上的任意一点,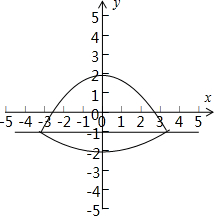
因为曲线C是平面内到定点F(0,1)和定直线l:y=-1的距离之和等于4的点的轨迹,
所以|PF|+|y+1|=4.即$\sqrt{{x}^{2}+(y-1)^{2}}$+|y+1|=4,
解得y≥-1时,y=2-$\frac{1}{4}$x2,当y<-1时,y=$\frac{1}{12}$x2-2;
显然①曲线C关于y轴对称;正确.
②若点P(x,y)在曲线C上,则|y|≤2;正确.
③若点P在曲线C上,|PF|+|y+1|=4,|y|≤2,则1≤|PF|≤4.正确.
故答案为:①②③.
点评 本题考查曲线轨迹方程的求法,曲线的基本性质的应用,考查计算能力.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
5.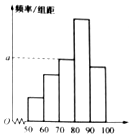 某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
(1)求表中t,q及图中a的值;
(2)该教师从这次考试成绩低于70分的学生中随机抽取3人进行面批,设X表示所抽取学生中成绩低于60分的人数,求随机变量X的分布列和数学期望.
 某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.| 分组 | 频数 | 频率 |
| [50,60) | 3 | 0.06 |
| [60,70) | m | 0.10 |
| [70,80) | 13 | n |
| [80,90) | p | q |
| [90,100] | 9 | 0.18 |
| 总计 | t | 1 |
(2)该教师从这次考试成绩低于70分的学生中随机抽取3人进行面批,设X表示所抽取学生中成绩低于60分的人数,求随机变量X的分布列和数学期望.
10.命题p:?x∈R,x≥0的否定是( )
| A. | ¬p:?x∈R,x<0 | B. | ¬p:?x∈R,x≤0 | C. | ¬p:?x∈R,x<0 | D. | ¬p:?x∈R,x≤0 |
20.设函数f(x)=sin(2x+$\frac{π}{4}$)(x∈[0,$\frac{9π}{8}$]),若方程f(x)=a恰好有三个根,分别为x1,x2,x3(x1<x2<x3),则x1+x2+x3的取值范围是( )
| A. | [$\frac{9π}{8}$,$\frac{5π}{4}$) | B. | [$\frac{5π}{4}$,$\frac{11π}{8}$) | C. | [$\frac{3π}{2}$,$\frac{13π}{8}$) | D. | [$\frac{7π}{4}$,$\frac{15π}{8}$) |
7.已知实数x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{4x-y-4≤0}\end{array}\right.$,则$\frac{y+2}{x+1}$的最大值为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 2 | D. | $\frac{5}{2}$ |