题目内容
已知四面体S-ABC中,SA=SB=2,且SA⊥SB,BC=
,AC=
,则该四面体的外接球的表面积为( )
| 5 |
| 3 |
| A、4π | ||||
B、
| ||||
C、
| ||||
| D、8π |
考点:球的体积和表面积
专题:空间位置关系与距离
分析:根据已知,结合勾股定理,可得AC⊥BC,取AB的中点O,根据直角三角形的性质,可得:OA=OB=OC=OD,即O为该四面体的外接球的球心,求出球半径后,代入表面积公式,可得答案.
解答:
解:∵SA=SB=2,且SA⊥SB,
∴AB=
=2
,
又∵BC=
,AC=
,
∴AC2+BC2=AB2,
即AC⊥BC,
取AB的中点O,
根据直角三角形的性质,可得:
OA=OB=OC=OD,
即O为该四面体的外接球的球心,
则该四面体的外接球的半径R=
AB=
,
故该四面体的外接球的表面积S=4πR2=8π,
故选:D
∴AB=
| SA2+SB2 |
| 2 |
又∵BC=
| 5 |
| 3 |
∴AC2+BC2=AB2,
即AC⊥BC,
取AB的中点O,
根据直角三角形的性质,可得:
OA=OB=OC=OD,
即O为该四面体的外接球的球心,
则该四面体的外接球的半径R=
| 1 |
| 2 |
| 2 |
故该四面体的外接球的表面积S=4πR2=8π,
故选:D
点评:本题考查的知识点是球的体积和表面积,其中根据已知求出球的半径是解答的关键.

练习册系列答案
相关题目
已知整数a,b,c,t满足:2a+2b=2c,t=
,则log2t的最大值是( )
| a+b |
| c |
| A、0 | B、log23 |
| C、2 | D、3 |
设等差数列{an}的前n项和为Sn,已知(a10-1)3+11a10=0,(a2-1)3+11a2=22,则下列结论正确的是( )
| A、S11=11,a10<a2 |
| B、S11=11,a10>a2 |
| C、S11=22,a10<a2 |
| D、S11=22,a10>a2 |
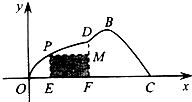 如图,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数y=k
如图,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数y=k