题目内容
①已知函数f（x）=
是（-∞，-1）上的增函数，求a的取值范围．
②定义在（-1，1）上的函数f（x）是增函数，且满足f（a-1）-f（3a）＜0，求a的取值范围．
| ax-2 |
| x+1 |
②定义在（-1，1）上的函数f（x）是增函数，且满足f（a-1）-f（3a）＜0，求a的取值范围．
考点：函数单调性的性质
专题：函数的性质及应用
分析：根据函数的单调性的定义进行求解．
解答：
解：①设任意的x1＜x2＜-1，
则f（x1）-f（x2）=
-
=（x1-x2）（a+2），
因函数f（x）=
是（-∞，-1）上的增函数，
∴f（x1）-f（x2）＜0
∴a+2＞0
即a＞-2；
②因定义在（-1，1）上的函数f（x）是增函数，且满足f（a-1）-f（3a）＜0，
所以f（a-1）＜f（3a），
∴
，
解得：0＜a＜
．
则f（x1）-f（x2）=
| ax1-2 |
| x1+1 |
| ax2-2 |
| x2+1 |
因函数f（x）=
| ax-2 |
| x+1 |
∴f（x1）-f（x2）＜0
∴a+2＞0
即a＞-2；
②因定义在（-1，1）上的函数f（x）是增函数，且满足f（a-1）-f（3a）＜0，
所以f（a-1）＜f（3a），
∴
|
解得：0＜a＜
| 1 |
| 3 |
点评：本题主要考查函数的单调性和单调性的应用，属于基础题．
练习册系列答案
相关题目
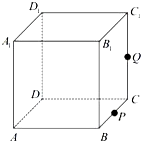如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则下列命题正确的是