题目内容
已知点P为直线l1:2x-3y-1=0和直线l2:x+y+2=0的交点,M(1,2),N(-1,-5).
(Ⅰ)求过点P 且与直线l3:3x+y-1=0平行的直线方程;
(Ⅱ)求过点P且与直线MN垂直的直线方程.
(Ⅰ)求过点P 且与直线l3:3x+y-1=0平行的直线方程;
(Ⅱ)求过点P且与直线MN垂直的直线方程.
考点:直线的一般式方程与直线的垂直关系,直线的一般式方程与直线的平行关系
专题:直线与圆
分析:(Ⅰ)利用两直线平行研究直线的斜率,再根据条件过点P,得到直线的方程;
(Ⅱ)利用两直线垂直研究直线的斜率,再根据条件过点P,得到直线的方程,得到本题结论.
(Ⅱ)利用两直线垂直研究直线的斜率,再根据条件过点P,得到直线的方程,得到本题结论.
解答:
解:由题意得:
(Ⅰ)
,解得:
,
∴P(-1,-1).
∵所求直线与直线l3:3x+y-1=0平行,
∴k=-3,
∴所求直线方程为:3x+y+4=0.
(Ⅱ)直线MN所在直线的斜率为:kMN=
=
,
∵所求直线与两点M(1,2),N(-1,-5)所在直线垂直,
∴k=-
,
则所求直线方程为:2x+7y+9=0.
(Ⅰ)
|
|
∴P(-1,-1).
∵所求直线与直线l3:3x+y-1=0平行,
∴k=-3,
∴所求直线方程为:3x+y+4=0.
(Ⅱ)直线MN所在直线的斜率为:kMN=
| -5-2 |
| -1-1 |
| 7 |
| 2 |
∵所求直线与两点M(1,2),N(-1,-5)所在直线垂直,
∴k=-
| 2 |
| 7 |
则所求直线方程为:2x+7y+9=0.
点评:本题考查了两直线平行和两直线垂直,本题难度不大,属于基础题.

练习册系列答案
相关题目
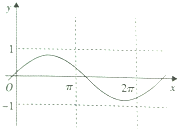
已知函数y=Asin(ωx+φ的图象如图所示,则该函数的解析式可能是( )

A、y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
