题目内容
9.已知数列{an},{bn}满足bn=an+1-an(n=1,2,3,…).(1)若bn=10-n,求a16-a5的值;
(2)若${b_n}={(-1)^n}({2^n}+{2^{33-n}})$且a1=1,则数列{a2n+1}中第几项最小?请说明理由;
(3)若cn=an+2an+1(n=1,2,3,…),求证:“数列{an}为等差数列”的充分必要条件是“数列{cn}为等差数列且bn≤bn+1(n=1,2,3,…)”.
分析 (1)判断{bn}是等差数列.然后化简a16-a5=(a16-a15)+(a15-a14)+(a14-a13)+…+(a6-a5)利用等差数列的性质求和即可.
(2)利用a2n+3-a2n+1=22n+1-231-2n,判断a2n+3<a2n+1,求出n<7.5,a2n+3>a2n+1求出n>7.5,带带数列{a2n+1}中a17最小,即第8项最小..
法二:化简${b_n}={(-1)^n}({2^n}+{2^{33-n}})={(-2)^n}+{2^{33}}{(-\frac{1}{2})^n}$,求出a2n+1=a1+b1+b2+b3+…+b2n=$\frac{1}{3}[1-{2^{33}}+({2^{2n+1}}+{2^{33-2n}})]$,利用基本不等式求出最小值得到数列{a2n+1}中的第8项最小.
(3)若数列{an}为等差数列,设其公差为d,说明数列{cn}为等差数列. 由bn=an+1-an=d(n=1,2,3,…),推出bn≤bn+1,若数列{cn}为等差数列且bn≤bn+1(n=1,2,3,…),设{cn}的公差为D,转化推出bn+1=bn(n=1,2,3,…),说明数列{an}为等差数列.得到结果.
解答 解:(1)由bn=10-n,可得bn+1-bn=(9-n)-(10-n)=-1,故{bn}是等差数列.
所以a16-a5=(a16-a15)+(a15-a14)+(a14-a13)+…+(a6-a5)=${b_{15}}+{b_{14}}+{b_{13}}+…+{b_5}=\frac{{11({b_{15}}+{b_5})}}{2}=11{b_{10}}=0$…(4分)
(2)a2n+3-a2n+1=(a2n+3-a2n+2)+(a2n+2-a2n+1)=b2n+2+b2n+1=(22n+2+231-2n)-(22n+1+232-2n)=22n+1-231-2n…(6分)
由a2n+3<a2n+1?22n+1-231-2n<0?n<7.5,a2n+3>a2n+1?22n+1-231-2n>0?n>7.5,…(8分)
故有a3>a5>a7>…>a15>a17<a19<a20<…,
所以数列{a2n+1}中a17最小,即第8项最小. …(10分)
法二:由${b_n}={(-1)^n}({2^n}+{2^{33-n}})={(-2)^n}+{2^{33}}{(-\frac{1}{2})^n}$,…(5分)
可知a2n+1=a1+b1+b2+b3+…+b2n=$1+[(-2)\frac{{1-{{(-2)}^{2n}}}}{3}+(-{2^{32}})\frac{{1-{{(-\frac{1}{2})}^{2n}}}}{{1+\frac{1}{2}}}]$=$\frac{1}{3}[1-{2^{33}}+({2^{2n+1}}+{2^{33-2n}})]$…(8分)$≥\frac{1}{3}[1-{2^{33}}+2\sqrt{{2^{34}}}]$(当且仅当22n+1=233-2n,即n=8时取等号)
所以数列{a2n+1}中的第8项最小. …(10分)
(3)若数列{an}为等差数列,设其公差为d,
则cn+1-cn=(an+1-an)+2(an+2-an+1)=d+2d=3d为常数,
所以数列{cn}为等差数列. …(12分)
由bn=an+1-an=d(n=1,2,3,…),可知bn≤bn+1(n=1,2,3,…). …(13分)
若数列{cn}为等差数列且bn≤bn+1(n=1,2,3,…),设{cn}的公差为D,
则cn+1-cn=(an+1-an)+2(an+2-an+1)=bn+2bn+1=D(n=1,2,3,…),…(15分)
又bn+1+2bn+2=D,故(bn+1-bn)+2(bn+2-bn+1)=D-D=0,
又bn+1-bn≥0,bn+2-bn+1≥0,故bn+1-bn=bn+2-bn+1=0(n=1,2,3,…),…(17分)
所以bn+1=bn(n=1,2,3,…),故有bn=b1,所以an+1-an=b1为常数.
故数列{an}为等差数列.
综上可得,“数列{an}为等差数列”的充分必要条件是“数列{cn}为等差数列且bn≤bn+1(n=1,2,3,…)”. …(18分)
点评 本题考查数列的综合应用,等差数列的性质等比数列的判断,数列求和,转化思想的应用,考查分析问题解决问题的能力.

| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{9}{10}$ | D. | $\frac{4}{5}$ |
| A. | 若p:?x∈R,ex>xe,q:?x0∈R,|x0|≤0,则(¬p)∧q为假 | |
| B. | x=1是x2-x=0的必要不充分条件 | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
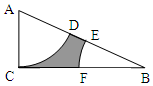 如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | $\frac{π}{8}$ | B. | 1-$\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
