题目内容
8．某产品的广告费用x（万元）与销售额y（万元）的统计数据如下表所示，根据表中的数据可得回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，其中$\widehat{a}$=0，据此模型预报，当广告费用为7万元时的销售额为（ ）| x | 4 | 2 | 3 | 5 |
| y | 38 | 20 | 31 | 51 |
| A． | 60 | B． | 70 | C． | 73 | D． | 69 |
分析 根据表中数据计算$\overline{x}$、$\overline{y}$，由回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$过样本中心点，求出$\widehat{b}$的值，再计算x=7时$\widehat{y}$的值即可．
解答 解：根据表中数据，得：$\overline{x}$=$\frac{1}{4}$×（4+2+3+5）=3.5，
$\overline{y}$=$\frac{1}{4}$×（38+20+31+51）=35；
且回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$过样本中心点（$\overline{x}$，$\overline{y}$），其中$\widehat{a}$=0，
所以$\widehat{b}$×3.5+0=35，解得$\widehat{b}$=10，
所以回归方程为$\widehat{y}$=10x；
当x=7时，$\widehat{y}$=10×7=70，
即广告费用为7万元时销售额为70万元．
故选：B．
点评 本题考查了线性回归方程的应用问题，是基础题目
练习册系列答案
相关题目
16．
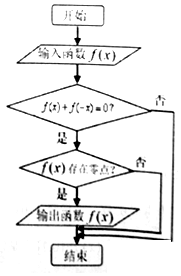程序框图如图所示，现输入如下四个函数：f（x）=$\frac{1}{x}$，f（x）=x4，f（x）=2x，f（x）=x-$\frac{1}{x}$，则可以输出的函数是（ ）
程序框图如图所示，现输入如下四个函数：f（x）=$\frac{1}{x}$，f（x）=x4，f（x）=2x，f（x）=x-$\frac{1}{x}$，则可以输出的函数是（ ）| A． | f（x）=$\frac{1}{x}$ | B． | f（x）=x4 | C． | f（x）=2x | D． | f（x）=x-$\frac{1}{x}$ |
3．将一枚质地均匀的硬币随机抛掷两次，出现一次正面向上，一次反面向上的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
3．已知抛物线C：y2=4x的交点为F，直线y=x-1与C相交于A，B两点，与双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=2（a＞0，b＞0）的渐近线相交于M，N两点，若线段AB与MN的中点相同，则双曲线E离心率为（ ）
| A． | $\frac{\sqrt{6}}{3}$ | B． | 2 | C． | $\frac{\sqrt{15}}{3}$ | D． | $\sqrt{3}$ |