题目内容
已知函数f(x)=
,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围为( )
|
| A、(1+e,1+e+e2) | ||||
B、(
| ||||
C、(2
| ||||
D、(2
|
考点:函数的图象
专题:函数的性质及应用
分析:画出函数的图象,判断a,b,c的范围,然后推出a+b+c的取值范围.
解答:
解:函数f(x)=
,若a,b,c互不相等,且f(a)=f(b)=f(c),如图,不妨a<b<c,
由已知条件可知:0<a<1<b<e<c<e2,
∵-lna=lnb,∴ab=1
∵lnb=2-1nc∴bc=e2,
∴a+b+c=b+
,(1<b<e),
令h(b)=b+
,(1<b<e),
由(b+
)′=1-
<0,故(1,e)为减区间,
∴2e+
<a+b+c<e2+2,
∴a+b+c的取值范围是:(
+2e,2+e2.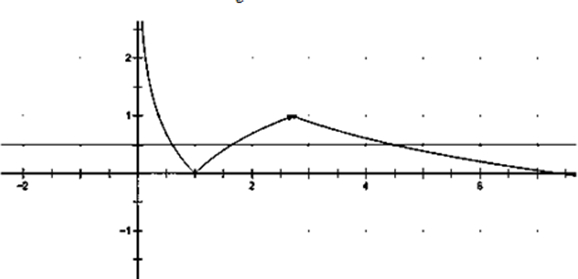
|
由已知条件可知:0<a<1<b<e<c<e2,
∵-lna=lnb,∴ab=1
∵lnb=2-1nc∴bc=e2,
∴a+b+c=b+
| e2+1 |
| b |
令h(b)=b+
| e2+1 |
| b |
由(b+
| e2+1 |
| b |
| e2+1 |
| b |
∴2e+
| 1 |
| e |
∴a+b+c的取值范围是:(
| 1 |
| e |

点评:本题考查函数的图象的应用,函数的零点的判定,基本知识的考查数形结合的应用.

练习册系列答案
相关题目
已知z1=1+i,且z1•(z1+z2)=4,则复数z2=( )
| A、1+i | B、1-i |
| C、1+3i | D、1-3i |
已知p:ea<eb,q:lna<lnb,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
(理)给出下列命题:
(1)已知事件A、B是互斥事件,若P(A)=0.25,P(B)=0.35,则P(A∪B)=0.60;
(2)已知事件A、B是互相独立事件,若P(A)=0.15,P(B)=0.60,则P(
B)=0.51(
表示事件A的对立事件);
(3)(
+
)18的二项展开式中,共有4个有理项.
则其中真命题的序号是( )
(1)已知事件A、B是互斥事件,若P(A)=0.25,P(B)=0.35,则P(A∪B)=0.60;
(2)已知事件A、B是互相独立事件,若P(A)=0.15,P(B)=0.60,则P(
. |
| A |
. |
| A |
(3)(
| 3 | x |
| 1 | ||
|
则其中真命题的序号是( )
| A、(1)(2) |
| B、(1)(3) |
| C、(2)(3) |
| D、(1)(2)(3) |
若复数z=(m2+2m-3)+(m-1)i是纯虚数(i是虚数单位),则实数m=( )
| A、-3 | B、3 | C、1 | D、1或-3 |
 如图,已知∠AOB在平面直角坐标系的第一象限中,且∠AOB=30°,其两边分别交反比例函数y=
如图,已知∠AOB在平面直角坐标系的第一象限中,且∠AOB=30°,其两边分别交反比例函数y=