题目内容
若y=f(x)是定义在R上周期为2的周期函数,且f(x)是偶函数,当x∈[0,1]时,f(x)=2x-1,则函数g(x)=f(x)-log3|x|的零点个数为 .
考点:根的存在性及根的个数判断,函数奇偶性的性质
专题:函数的性质及应用
分析:由g(x)=f(x)-log3|x|=0,得f(x)=log3|x|,利用条件求出函数f(x)的图象和性质,利用数形结合研究函数f(x)和y=log3|x|两个函数图象的交点即可确定函数的零点个数.
解答:
解:设x∈[-1,0],则-x∈[0,1],
则当x∈[0,1]时,f(x)=2x-1,
∴f(-x)=2-x-1,
∵函数f(x)是偶函数,
∴f(-x)=2-x-1=f(x),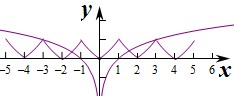
即f(x)=2-x-1,x∈[-1,0],
由g(x)=f(x)-log3|x|=0,得f(x)=log3|x|,
∵y=f(x)是定义在R上周期为2的周期函数,
∴作出函数f(x)和y=log3|x|的图象如图:
两个图象的交点个数为4个,
故函数零点个数为4个.
故答案为:4.
则当x∈[0,1]时,f(x)=2x-1,
∴f(-x)=2-x-1,
∵函数f(x)是偶函数,
∴f(-x)=2-x-1=f(x),

即f(x)=2-x-1,x∈[-1,0],
由g(x)=f(x)-log3|x|=0,得f(x)=log3|x|,
∵y=f(x)是定义在R上周期为2的周期函数,
∴作出函数f(x)和y=log3|x|的图象如图:
两个图象的交点个数为4个,
故函数零点个数为4个.
故答案为:4.
点评:本题主要考查了周期函数与对数函数的图象,数形结合是高考中常用的方法,考查数形结合.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
三个数0.993.3,log3π,log20.8的大小关系为( )
| A、log3π<0.993.3<log20.8 |
| B、log20.8<log3π<0.993.3 |
| C、log20.8<0.993.3<log3π |
| D、0.993.3<log20.8 l<log3π |