题目内容
16．定义在R上的偶函数f（x）满足：对任意的x1，x2∈（-∞，0）（x1≠x2），有$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}$＜0，则（ ）| A． | f（-3）＜f（-2）＜f（1） | B． | f（1）＜f（-2）＜f（-3） | C． | f（-2）＜f（1）＜f（-3） | D． | f（-3）＜f（1）＜f（-2） |
分析 确定f（x）在x1，x2∈（-∞，0]（x1≠x2）单调递减，在x1，x2∈[0，+∞）（x1≠x2）上单调递增，进而可判断出f（-3），f（-2）和f（1）的大小．
解答 解：∵对任意的x1，x2∈（-∞，0）（x1≠x2），有$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}$＜0，
∴f（x）在x1，x2∈（-∞，0]（x1≠x2）单调递减，
又f（x）是偶函数，故f（x）在x1，x2∈[0，+∞）（x1≠x2）上单调递增，．
∵f（-2）=f（2），f（-3）=f（3），3＞2＞1＞0，
∴f（1）＜f（-2）＜f（-3），
故选B．
点评 本题主要考查了函数奇偶性的应用和函数的单调性的应用．属基础题．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
7．将函数f（x）=sin2x的图象向右平移φ$（{0＜φ＜\frac{π}{2}}）$个单位后得到函数g（x）的图象，若g（x）在区间$[{0，\frac{π}{6}}]$上单调递增，且函数g（x）的最大负零点在区间$（{-\frac{π}{3}，-\frac{π}{6}}）$上，则φ的取值范围是（ ）
| A． | [$\frac{π}{12}$，$\frac{π}{4}$] | B． | [$\frac{π}{6}$，$\frac{5π}{12}$） | C． | [$\frac{π}{6}$，$\frac{π}{3}$] | D． | （$\frac{π}{6}$，$\frac{π}{4}$] |
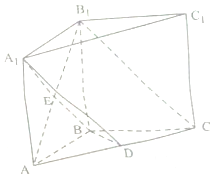如图，在直三棱柱ABC-A1B1C1中，AB=BC=BB1，AB1∩A1B=E，D为AC上的点，B1C∥平面A1BD．