题目内容
11．
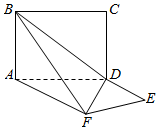平面ABCD⊥平面ADEF，其中ABCD为矩形，ADEF为梯形，AF∥DE，AF⊥FE，AF=AD=2DE=2，则异面直线EF与BC所成角大小为30°．
分析 延长AD，FE交于Q，∠AQF是异面直线EF与BC所成的角，由此能求出异面直线EF与BC所成角．
解答 
解：延长AD，FE交于Q．
∵ABCD是矩形，
∴BC∥AD，
∴∠AQF是异面直线EF与BC所成的角．
在梯形ADEF中，由DE∥AF，AF⊥FE，AF=2，DE=1得
∠AQF=30°．
即异面直线EF与BC所成角为30°．
故答案为：30°．
点评 本题考查异面直线所成角的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
2．设α∈（0，$\frac{π}{2}$），若sinα=$\frac{3}{5}$，则$\sqrt{2}$cos（α+$\frac{π}{4}$）等于（ ）
| A． | $\frac{7}{5}$ | B． | $\frac{1}{5}$ | C． | -$\frac{7}{5}$ | D． | -$\frac{1}{5}$ |
6．已知变量x，y满足$\left\{\begin{array}{l}{x+y≥1}\\{y-x≤1}\\{x≤1}\end{array}\right.$，则z=2x+2y的最小值为（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
16．已知函数$f（x）=\frac{4^x}{{{4^x}+1}}$，则f（-2016）+f（-2015）+…+f（-1）+f（0）+f（1）+f（2）+…+f（2015）+f（2016）=（ ）
| A． | 2016 | B． | 2017 | C． | $\frac{4033}{2}$ | D． | 4033 |